题目内容
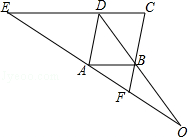
【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,边AO在y轴上,点B1 , B2 , B3 , …都在直线y= ![]() x上,则A2014的坐标是 .
x上,则A2014的坐标是 . 
【答案】(2014 ![]() ,2016)
,2016)
【解析】解:过B1向x轴作垂线B1C,垂足为C,
由题意可得:A(0,2),AO∥A1B1 , ∠B1OC=30°,
∴CO=OB1cos30°= ![]() ,
,
∴B1的横坐标为: ![]() ,则A1的横坐标为:
,则A1的横坐标为: ![]() ,
,
连接AA1 , 可知所有三角形顶点都在直线AA1上,
∵点B1 , B2 , B3 , …都在直线y= ![]() x上,AO=2,
x上,AO=2,
∴直线AA1的解析式为:y= ![]() x+2,
x+2,
∴y= ![]() ×
× ![]() +2=3,
+2=3,
∴A1( ![]() ,3),
,3),
同理可得出:A2的横坐标为:2 ![]() ,
,
∴y= ![]() ×2
×2 ![]() +2=4,
+2=4,
∴A2(2 ![]() ,4),
,4),
∴A3(3 ![]() ,5),
,5),
…
A2014(2014 ![]() ,2016).
,2016).
故答案为:(2014 ![]() ,2016).
,2016).
根据题意得出直线AA1的解析式为:y= ![]() x+2,进而得出A,A1 , A2 , A3坐标,进而得出坐标变化规律,进而得出答案.
x+2,进而得出A,A1 , A2 , A3坐标,进而得出坐标变化规律,进而得出答案.

练习册系列答案
相关题目