题目内容
 如图,在等腰直角△ABC中,AC=BC,点D在AB上.如果AD=AC,DE⊥AB与BC相交于点E,那么BD
如图,在等腰直角△ABC中,AC=BC,点D在AB上.如果AD=AC,DE⊥AB与BC相交于点E,那么BD分析:根据等腰三角形的性质求出∠A和∠B,根据多边形的内角和定理求出∠DEC,求出∠BED,推出BD=DE,连接AE,证△ADE和△ACE全等,推出DE=CE即可.
解答:解:∵DE⊥AB,
∴∠EDA=90°,
∵∠C=90°,AC=BC,
∴∠A=∠B=
(180°-∠C)=45°,
∴∠DEC=360°-∠EDA-∠A-∠C=135°,
∴∠BED=180°-∠DEC=45°=∠B,
∴BD=DE,
连接AE,
∵∠C=∠EDA=90°,AD=AC,AE=AE,
∴Rt△ADE≌Rt△ACE(HL),
∴DE=CE,
∴BD=CE.
故答案为:=.
∴∠EDA=90°,
∵∠C=90°,AC=BC,
∴∠A=∠B=
| 1 |
| 2 |
∴∠DEC=360°-∠EDA-∠A-∠C=135°,
∴∠BED=180°-∠DEC=45°=∠B,
∴BD=DE,

连接AE,
∵∠C=∠EDA=90°,AD=AC,AE=AE,
∴Rt△ADE≌Rt△ACE(HL),
∴DE=CE,
∴BD=CE.
故答案为:=.
点评:本题主要考查对等腰直角三角形的性质,三角形的内角和定理,多边形的内角和定理,全等三角形的性质和判定,等腰三角形的性质和判定等知识点的理解和掌握,能求出DE=BD和DE=CE是解此题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
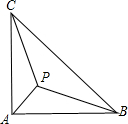 如图,在等腰直角三角形ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC=
如图,在等腰直角三角形ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC= 23、如图,在等腰直角三角形ABC和DEC中,∠BCA=∠BCE=90°,点E在边AB上,ED与AC交于点F,连接AD.
23、如图,在等腰直角三角形ABC和DEC中,∠BCA=∠BCE=90°,点E在边AB上,ED与AC交于点F,连接AD.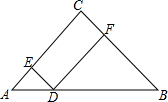 (2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( )
(2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( ) 如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.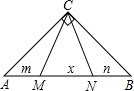 如图,在等腰直角△ABC的斜边AB上取两点M、N(不与A、B重合)使∠MCN=45°,记AM=m,MN=x,NB=n,试判断以x、m、n为边长的三角形的形状,并给予说明.
如图,在等腰直角△ABC的斜边AB上取两点M、N(不与A、B重合)使∠MCN=45°,记AM=m,MN=x,NB=n,试判断以x、m、n为边长的三角形的形状,并给予说明.