题目内容
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=6| 3 |
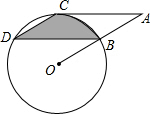
(1)求证:AC是⊙O的切线;
(2)求⊙O的半径长;
(3)求由弦CD、BD与弧BC所围成的阴影部分的面积(结果保留π).
分析:(1)连接CO,由角的等量关系可以证得∠ACO=90°,即能证得切线存在,
(2)由AC∥BD得到∠BEO=∠ACO=90°,在Rt△BEO中解得OB,
(3)首先证明△CDE≌△OBE,阴影部分面积等于S扇形OBC.
(2)由AC∥BD得到∠BEO=∠ACO=90°,在Rt△BEO中解得OB,
(3)首先证明△CDE≌△OBE,阴影部分面积等于S扇形OBC.
解答:(1)证明:连接CO.
∵∠CDB=∠OBD=30°,
∴∠BOC=60°.(1分)
∵AC∥BD,
∴∠A=∠OBD=30°.
∴∠ACO=90°.
∴AC为⊙O切线.(2分)
(2)解:∵∠ACO=90°,AC∥BD,
∴∠BEO=∠ACO=90°.
∴DE=BE=
BD=3
.(3分)
在Rt△BEO中,sin∠O=sin60°=
,
∴
=
.∴OB=6.
即⊙O的半径长为6cm.(4分)
(3)解:∵∠CDB=∠OBD=30°,
又∵∠CED=∠BEO,BE=ED,∴△CDE≌△OBE.
∴S阴=S扇OBC=
=6π(cm2)(5分)
答:阴影部分的面积为6πcm2.

∵∠CDB=∠OBD=30°,
∴∠BOC=60°.(1分)
∵AC∥BD,
∴∠A=∠OBD=30°.
∴∠ACO=90°.
∴AC为⊙O切线.(2分)
(2)解:∵∠ACO=90°,AC∥BD,
∴∠BEO=∠ACO=90°.
∴DE=BE=
| 1 |
| 2 |
| 3 |
在Rt△BEO中,sin∠O=sin60°=
| BE |
| OB |
∴
| ||
| 2 |
3
| ||
| OB |
即⊙O的半径长为6cm.(4分)
(3)解:∵∠CDB=∠OBD=30°,
又∵∠CED=∠BEO,BE=ED,∴△CDE≌△OBE.
∴S阴=S扇OBC=
| 60π×62 |
| 360 |
答:阴影部分的面积为6πcm2.
点评:本题考查了切线的判定,扇形面积的计算和解直角三角形等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 11、如图,点A、B、C都在⊙O上,若∠C=35°,则∠AOB=
11、如图,点A、B、C都在⊙O上,若∠C=35°,则∠AOB= 13、如图,点A、B、C都在00上,若∠C=40°,则∠AOB的度数为( )
13、如图,点A、B、C都在00上,若∠C=40°,则∠AOB的度数为( ) (2013•丰台区二模)如图,点A、B、C都在⊙O上,若∠AOB=68°,则∠ACB的度数为( )
(2013•丰台区二模)如图,点A、B、C都在⊙O上,若∠AOB=68°,则∠ACB的度数为( ) (2013•自贡)如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
(2013•自贡)如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB= 如图,点A、B、C都在⊙O上,连接AB、BC、AC、OA、OB,且∠BAO=25°,则∠ACB的大小为
如图,点A、B、C都在⊙O上,连接AB、BC、AC、OA、OB,且∠BAO=25°,则∠ACB的大小为