题目内容
某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A. 22+x=2×26
B. 22+x=2(26-x)
C. 2(22+x)=26-x
D. 22=2(26-x)
B 【解析】设第二组调到第一组x人,则第一组的现有人数为:(22+x)人,第二组的现有人数为:(26-x)人,又由于第一组现有人数是第二组的2倍,因此可列方程为: 22+x=2(26-x),故选B.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目


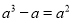 B.
B. 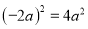 C.
C. 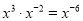 D.
D. 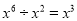
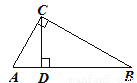
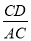 B.
B. 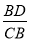 C.
C. 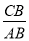 D.
D. 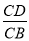
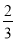 B. x=-
B. x=-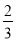 C. x=
C. x=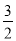 D. x=-
D. x=-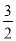
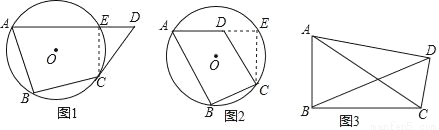
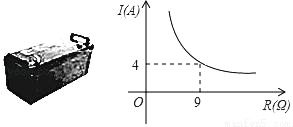
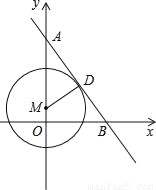
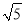 ,请写出点M的坐标,并写出以(﹣
,请写出点M的坐标,并写出以(﹣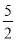 ,
, 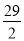 )为顶点,且过点M的抛物线的解析式.
)为顶点,且过点M的抛物线的解析式.