题目内容
已知直线x-y-1=0与抛物线y=ax2相切,则a=
- A.

- B.

- C.

- D.

A
分析:直线x-y-1=0与抛物线y=ax2相切,即它们只有一个公共点,可把y=x-1代入y=ax2,得到一个关于x的一元二次方程,则方程有两个相等的实数解,即判别式为0,从而求出a的值.
解答:把y=x-1代入y=ax2,
得ax2-x+1=0,
∴△=b2-4ac=(-1)2-4×a×1=0,
∴a= .
.
故选A.
点评:直线与抛物线相切是指它们只有一个公共点,即它们有公共解,可把方程进行转化,利用判别式求出a的值.
分析:直线x-y-1=0与抛物线y=ax2相切,即它们只有一个公共点,可把y=x-1代入y=ax2,得到一个关于x的一元二次方程,则方程有两个相等的实数解,即判别式为0,从而求出a的值.
解答:把y=x-1代入y=ax2,
得ax2-x+1=0,
∴△=b2-4ac=(-1)2-4×a×1=0,
∴a=
 .
.故选A.
点评:直线与抛物线相切是指它们只有一个公共点,即它们有公共解,可把方程进行转化,利用判别式求出a的值.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
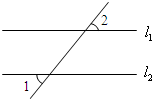 (2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2=
(2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2= (2012•株洲模拟)如图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC的度数为( )
(2012•株洲模拟)如图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC的度数为( )
 如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=8,则AB、CD之间的距离为
如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=8,则AB、CD之间的距离为