题目内容
18. 甲、乙两车从A地出发前往B地.汽车离开A地的距离 y(km)与时间t(h)的关系如图所示.
甲、乙两车从A地出发前往B地.汽车离开A地的距离 y(km)与时间t(h)的关系如图所示.(1)乙车的平均速度是100km/h;
(2)求图中a的值;
(3)当两车相距20km时,甲车行驶了$\frac{8}{3}$或4小时.
分析 (1)由速度=路程÷时间就可以求得乙的速度;
(2)由函数图象的数据求出两车相遇的时间就可以求出路程a的值;
(3)由追击问题的数量关系建立方程就可以求出两车相距20km时t的值.
解答 解:(1)由题意,得:乙车的平均速度为:350÷(4.5-1)=100km/h;
故答案为:100km/h;
(2)∵甲车的速度为:350÷5=70km/h,
设乙出发x小时追上甲车,由题意,得:70(x+1)=100x,
解得:x=$\frac{7}{3}$,
∴a=$\frac{7}{3}$×100=$\frac{700}{3}$km.
(3)当两车相距20km时,①70t-100(t-1)=20,解得:t=$\frac{8}{3}$.
②100(t-1)-70t=20,解得:t=4.
∴当两车相距20km时,甲车行驶了$\frac{8}{3}$或4时.
故答案为:$\frac{8}{3}$或4.
点评 本题考查了行程问题的追击问题的数量关系的运用,属于一次函数的图象的运用.注意解答时分析清楚函数图象的数据的含义是关键.

练习册系列答案
相关题目
7.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是( )


| A. | 轴对称变换 | B. | 平移变换 | C. | 旋转变换 | D. | 中心对称变换 |
8.要使式子$\sqrt{\frac{1}{x+2}}$有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x≤-2 | C. | x>-2 | D. | x<-2 |
 如图,在平面直角坐标系中,O为坐标原点,点A(4,1),B(1,1)C(4,5),D(6,-3),E(-2,5)
如图,在平面直角坐标系中,O为坐标原点,点A(4,1),B(1,1)C(4,5),D(6,-3),E(-2,5)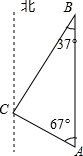 如图,某轮船位于A处,观测到某港口城市C位于轮船的北偏西67°,轮船以21海里/时的速度向正北方向行驶,行驶5小时后该船到达B处,这时观测到城市C位于该船的南偏西37°方向,求此时轮船所处位置B与城市C的距离.
如图,某轮船位于A处,观测到某港口城市C位于轮船的北偏西67°,轮船以21海里/时的速度向正北方向行驶,行驶5小时后该船到达B处,这时观测到城市C位于该船的南偏西37°方向,求此时轮船所处位置B与城市C的距离.