题目内容
【题目】如图，△ABC是边长为2的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作s1；取BE中点E1，作E1D1∥FB，E1F1∥EF，得到四边形E1D1FF1，它的面积记作s2．照此规律作下去，则s2019＝_____．
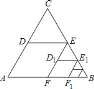
【答案】
.
【解析】
先根据已知条件计算出△ABC的高，再利用中位线定理求得AF的长，进而求得s1；同理可得s2…根据规律可写出Sn，再将n取2019代入计算即可得答案．
解：∵△ABC是边长为2的等边三角形，
∴△ABC的高为：2×sin60°＝2×
＝
，
∵DE、EF是△ABC的中位线，
∴AF＝1，易得四边形EDAF是平行四边形，
∴S1＝1×
×＝
，
同理可得S2＝×
＝，…，
∴Sn＝×
，
∴S2019＝×
=
=，
故答案为：．
练习册系列答案
相关题目
