题目内容
 在Rt△ABC中,∠ACB=90°,AB=5,
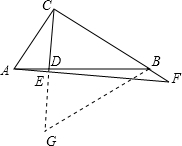
在Rt△ABC中,∠ACB=90°,AB=5, ,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE交直线BC于点F.
,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE交直线BC于点F.
(1)当 时,求线段BF的长;
时,求线段BF的长;
(2)当点F在边BC上时,设AD=x,BF=y,求y关于x的函数解析式,及其定义域;
(3)当 时,求线段AD的长.
时,求线段AD的长.
解:(1)在△ABC中,∠ACB=90°,AB=5, ,
,
∴BC=4,AC=3,
∵AE⊥CD,∠ACB=90°,
∴∠BCD+∠AFC=90°,∠AFC+∠CAF=90°,
∴∠CAF=∠BCD
∴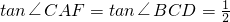 ,
,
又∵∠ACB=90°,AC=3,
∴CF= ,BF=
,BF=
(2)过点B作BG∥AC,交CD延长线于点G,
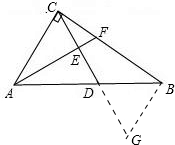
∴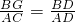 ,即
,即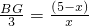 ①
①
在Rt△ACF与Rt△CBG中,
由(1)得tan∠CAF=tan∠BCD,
∴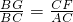 ,即
,即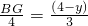 ,②
,②
由①②得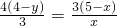 ,
,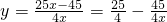
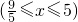
(3)1°当点F在线段BC上时,
把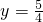 代入
代入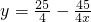 解得
解得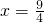 ,
,
2°当点F在CB延长线上时,
设AD=x,由(2)同理可得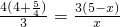 ,解得
,解得
综上所述当 时,线段AD的长为
时,线段AD的长为 或
或
分析:(1)由题意先求出AC,BC的长,由AE⊥CD和∠ACB=90°,证明出∠CAF=∠BCD,再由 ,可知
,可知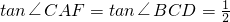 ,求得CF,从而求得线段BF的长;
,求得CF,从而求得线段BF的长;
(2)通过分析,作辅助线,过点B作BG∥AC,交CD延长线于点G,根据平行线的性质得: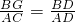 ,再由(1)得
,再由(1)得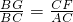 ,根据以上两个式子求出y关于x的函数解析式,
,根据以上两个式子求出y关于x的函数解析式,
(3)分两种情况:①当点F在线段BC上时,②当点F在CB延长线上时,求得线段AD的长为 或
或 .
.
点评:本题主要考查了三角函数的应用,用到了分类讨论的思想,是一道综合题难度大.
 ,
,∴BC=4,AC=3,
∵AE⊥CD,∠ACB=90°,
∴∠BCD+∠AFC=90°,∠AFC+∠CAF=90°,
∴∠CAF=∠BCD
∴
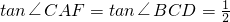 ,
,又∵∠ACB=90°,AC=3,
∴CF=
 ,BF=
,BF=
(2)过点B作BG∥AC,交CD延长线于点G,

∴
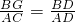 ,即
,即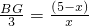 ①
①在Rt△ACF与Rt△CBG中,
由(1)得tan∠CAF=tan∠BCD,

∴
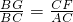 ,即
,即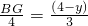 ,②
,②由①②得
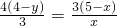 ,
,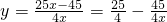
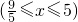
(3)1°当点F在线段BC上时,
把
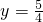 代入
代入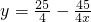 解得
解得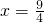 ,
,2°当点F在CB延长线上时,
设AD=x,由(2)同理可得
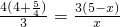 ,解得
,解得
综上所述当
 时,线段AD的长为
时,线段AD的长为 或
或
分析:(1)由题意先求出AC,BC的长,由AE⊥CD和∠ACB=90°,证明出∠CAF=∠BCD,再由
 ,可知
,可知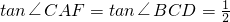 ,求得CF,从而求得线段BF的长;
,求得CF,从而求得线段BF的长;(2)通过分析,作辅助线,过点B作BG∥AC,交CD延长线于点G,根据平行线的性质得:
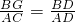 ,再由(1)得
,再由(1)得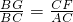 ,根据以上两个式子求出y关于x的函数解析式,
,根据以上两个式子求出y关于x的函数解析式,(3)分两种情况:①当点F在线段BC上时,②当点F在CB延长线上时,求得线段AD的长为
 或
或 .
.点评:本题主要考查了三角函数的应用,用到了分类讨论的思想,是一道综合题难度大.

练习册系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )