Question

如图，CD，BE是△ABC的角平分线，∠A=60°，BD=2CE=2，则△ABC的周长是________．

Answer 1

分析：过B作BQ∥AC交CD的延长线于Q，在BC上截取BF=BD=2，由BE平分∠ABC，CD平分∠ACB，得出∠SBC=∠ABC，∠DCB=∠ACB=∠ACD，求出∠SBC+∠DCB=60°，求出∠ADS+∠AES=360°-（∠A+∠DSE）=180°，根据SAS证△BDS≌△BFS，得出∠BDS=∠BFS，根据邻补角的定义求出∠CFS=∠ESC，证△CES≌△CFS，求出BC=1+2=3，由BQ∥AC，求出BC=BQ=3，和=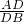，推出==，设AC=3x，AD=2x，根据BC²=AB²+AC²-2AB•ACcosA，求出x=，求出AC=，AB=，根据△ABC的周长是AB+BC+AC求出即可．
解答：解：过B作BQ∥AC交CD的延长线于Q，在BC上截取BF=BD=2，
∵BE平分∠ABC，CD平分∠ACB，
∴∠SBC=∠ABC，∠DCB=∠ACB=∠ACD，
∴∠SBC+∠DCB=（∠ABC+∠ACB），
=（180°-∠A）=60°，
∴∠BSC=180°-（∠SBC+∠SCB）=120°，
∴∠DSE=∠BSC=120°，
∴∠ADS+∠AES=360°-（∠A+∠DSE）=180°，
∵BD=BF，∠ABE=∠CBE，SB=SB，
∴△BDS≌△BFS，
∴∠BDS=∠BFS，
∵∠ADS+∠BDS=180°，∠BFS+∠CFS=180°，∠AES+∠CES=180°，
∴∠CFS=∠ESC，
∵∠ACD=∠BCD，CS=CS，
∴△CES≌△CFS，
∴CF=CE=1，
∴BC=1+2=3，
∵BQ∥AC，
∴∠Q=∠ACD=BCD，
∴BC=BQ=3，
∴=，
==，
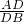设AC=3x，AD=2x，
∵BC²=AB²+AC²-2AB•ACcosA，
∴3²=（2+2x）²+（3x）²-2（2+2x）•3xcos60°，
∵x＞0，
解得：x=，
∴AC=，AB=2+=，
∴△ABC的周长是AB+BC+AC=，
答：△ABC的周长是．
点评：本题主要考查对三角形的内角和定理，多边形的内角和定理，对顶角和邻补角，等腰三角形的判定，平行线分线段成比例定理，平行线的性质，角平分线的性质，三角形的内切圆与内心，全等三角形的性质和判定，余弦定理等知识点的理解和掌握，综合运用这些性质进行推理是解此题的关键，此题是一个拔高的题目，难度偏大．