题目内容
已知正比例函数y=kx的函数值y随自变量x的增大而增大,那么一次函数y=-kx-2的图象不经过第 象限.
考点:一次函数图象与系数的关系
专题:
分析:先根据正比例函数y=kx的函数值y随自变量x的增大而增大判断出k的符号,再根据一次函数的图象与系数的关系判断出一次函数y=-kx-2的图象所经过的象限,进而可得出结论.
解答:解:∵正比例函数y=kx的函数值y随自变量x的增大而增大,
∴k>0,
∴-k<0,
又-2<0,
∴一次函数y=-kx-2的图象经过二、三、四象限,不经过第一象限.
故答案为:一.
∴k>0,
∴-k<0,
又-2<0,
∴一次函数y=-kx-2的图象经过二、三、四象限,不经过第一象限.
故答案为:一.
点评:本题考查的是一次函数的图象与系数的关系,由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.
①k>0,b>0?y=kx+b的图象在一、二、三象限;
②k>0,b<0?y=kx+b的图象在一、三、四象限;
③k<0,b>0?y=kx+b的图象在一、二、四象限;
④k<0,b<0?y=kx+b的图象在二、三、四象限.
①k>0,b>0?y=kx+b的图象在一、二、三象限;
②k>0,b<0?y=kx+b的图象在一、三、四象限;
③k<0,b>0?y=kx+b的图象在一、二、四象限;
④k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果水位下降5米记作-5米,那么水位上升4米,记作( )
| A、1米 | B、7米 | C、4米 | D、-7米 |
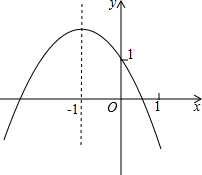 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0;②a-b>m(am+b)(其中m≠-1);③a2+c2<b2-2ac;④4a-2b+c<0;⑤c-a>1.
其中结论正确的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,把△ABC绕点A沿顺时针旋转75°,把点B转到点E得△AEF,则以下结论错误的是( )
如图,把△ABC绕点A沿顺时针旋转75°,把点B转到点E得△AEF,则以下结论错误的是( )| A、∠BAE=75° |
| B、AC=AF |
| C、EF=BC |
| D、∠EAF=75° |
 如图所示,AB是圆中的一条弦,C是圆上(不同于A、B)的点,过B的切线与AC的延长线交于P点,Q是
如图所示,AB是圆中的一条弦,C是圆上(不同于A、B)的点,过B的切线与AC的延长线交于P点,Q是
 已知,如图,在?ABCD中,E为AD上一点,EF∥AC交CD于点F,BF的延长线交AD的延长线于G.求证:AD2=AE•AG.
已知,如图,在?ABCD中,E为AD上一点,EF∥AC交CD于点F,BF的延长线交AD的延长线于G.求证:AD2=AE•AG.