题目内容
【题目】如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在X轴、Y轴上，连结OB，将纸片OABC沿OB折叠，使点A落在A’的位置，若OB＝
，tan∠COB＝
，则点A’的坐标为______。
【答案】
【解析】
试题分析：设OC与A′B交于点F，作A′E⊥OC于点E，
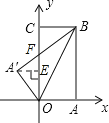
∵ OB＝
，tan∠COB＝
，∴BC=1，OC=2，∵纸片OABC沿OB折叠，∴OA=OA′，∠BAO=∠BA′O=90°，∵BC∥A′E，∴∠CBF=∠FA′E，∵∠AOE=∠FA′O，∴∠A′OE=∠CBF，∴△BCF≌△OA′F，∴OA′=BC=1，设A′F=x，∴OF=2-x∴x2+1=（2-x）2，解得x=
，∴A′F=
，OF=
，∵A′E=A′F×OA′÷OF=
，∴OE=
，∴点A’的坐标为（
，
）．
练习册系列答案
相关题目
