题目内容
如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(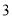 ,
, ),与y轴交于C(
),与y轴交于C( ,
, )点,点P是直线BC下方的抛物线上一动点.
)点,点P是直线BC下方的抛物线上一动点.

(1)求这个二次函数的解析式;
(2)若抛物线的顶点为点D,求△BCD的面积;
(3)设M是(1)所得抛物线上第四象限内的一个动点,过点M作直线l⊥x 轴于点F,交直线BC于点N。试问:线段MN的长度是否存在最大值?若存在,求出它最大值及此时M点的坐标;若不存在,请说明理由.
(1)y=x2﹣2x﹣3;(2)3;(3) 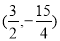
【解析】
试题分析:(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;(2)过点D作DE⊥y轴于点E,则∠DEC=∠BOC=90°根据B(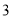 ,
,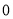 ),C(
),C(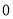 ,
,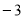 )可得OB=3,OC=3 把y=x2﹣2x﹣3 配方的为:
)可得OB=3,OC=3 把y=x2﹣2x﹣3 配方的为: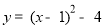 求出顶点D(1,-4),所以可得OE=4,DE=1 ,CE=OE-OC=4-3=1,从而求出△BCD的面积
求出顶点D(1,-4),所以可得OE=4,DE=1 ,CE=OE-OC=4-3=1,从而求出△BCD的面积
(3)设直线BC的关系式为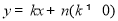 ,将 B(
,将 B(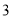 ,
,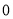 ),C(
),C(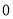 ,
,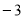 )带入
)带入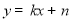 中,求得直线DE的关系式为
中,求得直线DE的关系式为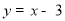 ,根据点M在抛物线上,点N在直线BC上,MN⊥x 轴于点F,M、N在第四象,求出线段MN长度有最大值即可求出此时M点的坐标
,根据点M在抛物线上,点N在直线BC上,MN⊥x 轴于点F,M、N在第四象,求出线段MN长度有最大值即可求出此时M点的坐标
试题解析:【解析】
(1)将B(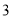 ,
,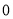 ),C(
),C(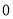 ,
,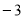 )两点的坐标代入得 :
)两点的坐标代入得 :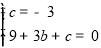
解得:b=-2,c=-3;
所以二次函数的表达式为:y=x2﹣2x﹣3
(2)过点D作DE⊥y轴于点E,则∠DEC=∠BOC=90°
∵B(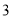 ,
,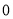 ),C(
),C(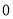 ,
,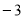 )∴OB=3,OC=3
)∴OB=3,OC=3
y=x2﹣2x﹣3 配方的: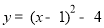
∴D(1,-4)
∴OE=4,DE=1 ∴CE=OE-OC=4-3=1
∴ 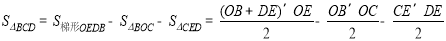
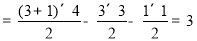 .
.
(3)设直线BC的关系式为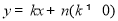
将 B(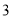 ,
,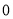 ),C(
),C(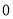 ,
,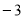 )带入
)带入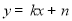 中
中
则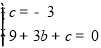
解得k=1,n=-3
∴直线DE的关系式为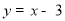
∵点M在抛物线上,点N在直线BC上
又∵MN⊥x 轴于点F,M、N在第四象限
∴设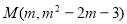 、
、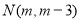
∴MF=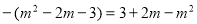 ,NF=
,NF=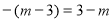
∴MN=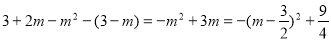
∴当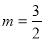 时,线段MN长度有最大值为
时,线段MN长度有最大值为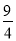 ,此时M的坐标为
,此时M的坐标为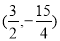
考点:1.待定系数法二次函数解析式的确定;2二次函数的性质;3.图形面积的求法

 ,其中
,其中 是方程
是方程 的解.
的解. 的根是 ;
的根是 ; 

 ;
;
 的相反数是( )
的相反数是( )  B、
B、 C、
C、 D、
D、
 取3)是( )
取3)是( )