题目内容
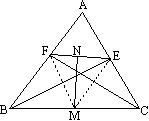
如图所示,BE、CF是△ABC的两条高,M是BC的中点,N是EF的中点.求证:MN⊥EF.
答案:
解析:
解析:
|
证明:连接 EM、FM,∵BE、CF是△ABC的高,∴∠BFC=∠BEC=Rt∠.∴△BEC和△BFC都是Rt△.又∵M是两直角三角形公共的斜边上的中点.∴FM=EM=解析: N是EF的中点,要证明MN⊥EF,只要证明MF=ME.利用等腰三角形底边上的高与中线重合的性质来达到目的.由已知条件不难分析出EM、FM分别是Rt△BCE和Rt△BCF斜边上的中线,显然它们都是BC的一半,这样就得到了解题思路. |

练习册系列答案
相关题目
 如图所示,BE、CF是直线,OA、OD是射线,其中构成对顶角的是( )
如图所示,BE、CF是直线,OA、OD是射线,其中构成对顶角的是( )
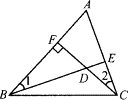
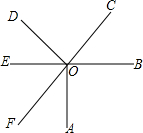 如图所示,BE、CF是直线,OA、OD是射线,其中构成对顶角的是
如图所示,BE、CF是直线,OA、OD是射线,其中构成对顶角的是