��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() �ֱ���
�ֱ���![]() ���������
���������![]() ���������ϣ���
���������ϣ���![]() ����
����![]() ��ԭ�������ÿ��
��ԭ�������ÿ��![]() ����λ���ȵ��ٶ���x�������᷽���˶���
����λ���ȵ��ٶ���x�������᷽���˶���

��1�����![]() �����꣮
�����꣮
��2������![]() ��������
��������![]() �����Ϊ
�����Ϊ![]() ����
����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �����ú�
�����ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() ��ֱ��д��
��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3������![]() ��
��![]() ���˶�ʱ�����߶�
���˶�ʱ�����߶�![]() ��
��![]() ��������ƽ�ƣ�ʹ��
��������ƽ�ƣ�ʹ��![]() ���
���![]() �غϣ���
�غϣ���![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() ������
������![]() �����߶�
�����߶�![]() ��
��![]() ��������ƽ�ƣ�ʹ��
��������ƽ�ƣ�ʹ��![]() ���
���![]() �غϣ���
�غϣ���![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() ��ȡ
��ȡ![]() ���е�
���е�![]() �Ƿ����
�Ƿ����![]() ��ֵ��ʹ������
��ֵ��ʹ������![]() ���������������
���������������![]() ������������ڣ����
������������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ��
��![]() ��2��
��2�� ��3������
��3������![]() ��ֵ��ʹ������
��ֵ��ʹ������![]() ���������������
���������������![]() �������
�������![]() ���
���![]() ��
��
��������
��1�����ݾ���ֵ�ķǸ��ԡ�ƽ���ķǸ��Եõ�����![]() ��
��![]() �ķ����飬�ⷽ���鼴�ɵý⣻
�ķ����飬�ⷽ���鼴�ɵý⣻
��2�����������֪��Ե�![]() ��λ�ý��з������ۣ��ֱ���Ӧ��ͼ�Σ�Ȼ���ٷֱ��ʾ������Ӧ�Ĺ�ϵʽ�Լ��Ա�����ȡֵ��Χ���ɣ�
��λ�ý��з������ۣ��ֱ���Ӧ��ͼ�Σ�Ȼ���ٷֱ��ʾ������Ӧ�Ĺ�ϵʽ�Լ��Ա�����ȡֵ��Χ���ɣ�
��3���ڣ�2���Ļ����϶Ե�![]() ��λ�ý��з������ۣ��ֱ�Ҫ����Ӧ��ͼ�Σ�Ȼ��ֱ�ʹ
��λ�ý��з������ۣ��ֱ�Ҫ����Ӧ��ͼ�Σ�Ȼ��ֱ�ʹ![]() ���Ӷ��õ�����
���Ӷ��õ�����![]() �ķ��̣��ⷽ�̼��ɵý⣮
�ķ��̣��ⷽ�̼��ɵý⣮
�⣺��1����![]()
��![]()
��![]()
��![]() ��
��![]() ��
��
��2����![]() ��
��![]()
��![]() ��
��![]()
�ٵ���![]() ���߶�
���߶�![]() ��ʱ����ͼ��
��ʱ����ͼ��

�ߵ�![]() ��ԭ�������ÿ��
��ԭ�������ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() �������᷽���˶�
�������᷽���˶�
���![]() �˶���
�˶���![]() ��ʱ��
��ʱ��![]()
��![]()
��![]()
�ߵ�![]() ���߶�
���߶�![]() ��
��
��![]()
�൱��![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��![]() ��
��
�ڵ���![]() ���߶�
���߶�![]() �ӳ�����ʱ����ͼ��
�ӳ�����ʱ����ͼ��

�ߵ�![]() ��ԭ�������ÿ��
��ԭ�������ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() �������᷽���˶�
�������᷽���˶�
���![]() �˶���
�˶���![]() ��ʱ��
��ʱ��![]()
��![]()
��![]()
�ߵ�![]() ���߶�
���߶�![]() �ӳ�����
�ӳ�����
��![]()
�൱��![]() ���߶�
���߶�![]() �ӳ�����ʱ��
�ӳ�����ʱ��![]()
������������ ��
��
��3����![]() ��
��![]() ��
��![]()
��![]()
�ߵ�![]() ��
��![]() ���е�
���е�
��![]()
�߹���![]() ��
��![]() �ڵ�
�ڵ�![]()
��![]() ��
��![]()
��![]()
�ٵ���![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��![]() ����ͼ��
����ͼ��

��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() �룻
�룻
�ڵ���![]() ���߶�
���߶�![]() �ӳ�����ʱ��
�ӳ�����ʱ��![]() ����ͼ��
����ͼ��

��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() �룻
�룻
����������������![]() ��ֵ��ʹ������
��ֵ��ʹ������![]() ���������������
���������������![]() �������
�������![]() ���
���![]() �룮
�룮

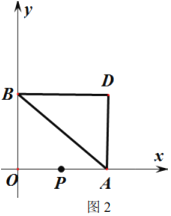
����Ŀ����֪������A1B1C1����������ABC����ƽ�Ƶõ��ģ�����A��B��C����Ķ�Ӧ��ֱ���A1��B1��C1��������ƽ��ֱ������ϵ�е����������ʾ��
������ABC | A��0��0�� | B����1��2�� | C��2��5�� |
������A1B1C1 | A1��a��2�� | B1��4��b�� | C1��7��7�� |
��1���۲���и���Ӧ������ı仯�����a=����������b=����������
��2����ͼ�е�ƽ��ֱ������ϵ�л���������ABC��������A1B1C1��
��3��P��m��n��Ϊ������ABC������һ�㣬��ƽ�ƺ��Ӧ��P'������Ϊ����������