Question

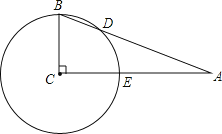
【题目】如图，在直角中，，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E．

若，求弧DE的度数；

若，，求BD的长．

Answer 1

【答案】(1)40°（2）

【解析】

（1）求出∠B的度数，求出∠B所对的弧的度数，即可得出答案；

（2）作CH⊥BD，如图，根据垂径定理得到BH=DH，再利用勾股定理计算出AB=15，接着利用面积法计算出CH=，然后利用勾股定理计算出BH，从而得到BD的长.

解：（1）连接CD，

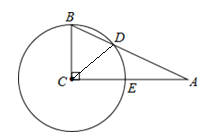
∵在△ABC中，∠C=90°，∠A=25°，

∴∠B=65°，

∵BC=CD,

∴∠BDC=65°,

∴∠BCD=50°，

∴弧DE的度数是90°-50°=40°；

（2）作CH⊥BD，如图，则BH=DH，

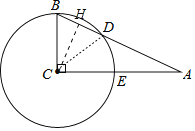
在Rt△ACB中，AB===，

∵ CHAB=BCAC，

∴CH==，

在Rt△BCH中，BH==，

∴BD=2BH=.