题目内容
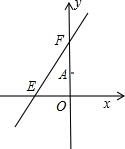
如图，A、B两点坐标分别是（4，0），（0，3），M是y轴上一点，沿AM折叠，AB刚好落在x轴上AB′处，则直线AM的解析式为______．
易得AB=5，
∴AB′=5，
∴OB′=1，
由折叠可得BM=B′M，
∴OM2+OB′2=B′M2，即OM2+12=（3-OM）2，
解得OM=
．
设AM的解析式为y=kx+
，
∴4k+
=0，
解得k=-
，
∴y=-
x+
．
故答案为y=-
x+
．
∴AB′=5，
∴OB′=1，
由折叠可得BM=B′M，
∴OM2+OB′2=B′M2，即OM2+12=（3-OM）2，
解得OM=
| 4 |
| 3 |
设AM的解析式为y=kx+
| 4 |
| 3 |
∴4k+
| 4 |
| 3 |
解得k=-
| 1 |
| 3 |
∴y=-
| 1 |
| 3 |
| 4 |
| 3 |
故答案为y=-
| 1 |
| 3 |
| 4 |
| 3 |
练习册系列答案
相关题目
，3）．
交于点A．
情况下，饮水机水桶内的存水量y（升）与接水时间x（分）的函数关系图象如图所示．请结合图象回答下列问题：
是否改变？若不变，请指出来；若改变，请写出面积变化的范围．（不必说明理由）