题目内容
 (1)如图1,在△ABC中,∠C=90°,∠BAC=45°,∠BAC的平分线与外角∠CBE的平分线相交于点D,则∠D=
(1)如图1,在△ABC中,∠C=90°,∠BAC=45°,∠BAC的平分线与外角∠CBE的平分线相交于点D,则∠D=(2)如图2,将(1)中的条件“∠BAC=45°”去掉,其他条件不变,求∠D的度数.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)由三角形外角的性质,可得∠C=∠CBE-∠CAB,∠D=∠2-∠1,又由∠BAC的平分线与外角∠CBE的平分线相交于点D,根据角平分线的性质,可得∠1=
∠CAB,∠2=
∠CBE,继而可求得答案;
(2)由三角形外角的性质,可得∠C=∠CBE-∠CAB,∠D=∠2-∠1,又由∠BAC的平分线与外角∠CBE的平分线相交于点D,根据角平分线的性质,可得∠1=
∠CAB,∠2=
∠CBE,继而可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由三角形外角的性质,可得∠C=∠CBE-∠CAB,∠D=∠2-∠1,又由∠BAC的平分线与外角∠CBE的平分线相交于点D,根据角平分线的性质,可得∠1=
| 1 |
| 2 |
| 1 |
| 2 |
解答: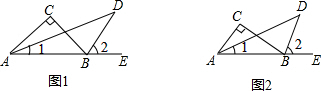 解:(1)∵∠CBE是△ABC的外角,
解:(1)∵∠CBE是△ABC的外角,
∴∠CBE=∠CAB+∠C,
∴∠C=∠CBE-∠CAB,
∵∠BAC的平分线与外角∠CBE的平分线相交于点D,
∴∠1=
∠CAB,∠2=
∠CBE,
∵∠2是△ABD的外角,
∴∠2=∠1+∠D,
∴∠D=∠2-∠1=
(∠CBE-∠CAB)=
∠C=
×90°=45°;
故答案为:45;
(2)∵∠CBE是△ABC的外角,
∴∠CBE=∠CAB+∠C,
∴∠C=∠CBE-∠CAB,
∵∠BAC的平分线与外角∠CBE的平分线相交于点D,
∴∠1=
∠CAB,∠2=
∠CBE,
∵∠2是△ABD的外角,
∴∠2=∠1+∠D,
∴∠D=∠2-∠1=
(∠CBE-∠CAB)=
∠C=
×90°=45°.
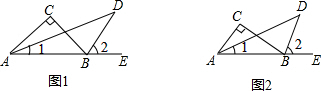 解:(1)∵∠CBE是△ABC的外角,
解:(1)∵∠CBE是△ABC的外角,∴∠CBE=∠CAB+∠C,
∴∠C=∠CBE-∠CAB,
∵∠BAC的平分线与外角∠CBE的平分线相交于点D,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠2是△ABD的外角,
∴∠2=∠1+∠D,
∴∠D=∠2-∠1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:45;
(2)∵∠CBE是△ABC的外角,
∴∠CBE=∠CAB+∠C,
∴∠C=∠CBE-∠CAB,
∵∠BAC的平分线与外角∠CBE的平分线相交于点D,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠2是△ABD的外角,
∴∠2=∠1+∠D,
∴∠D=∠2-∠1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了三角形外角的性质与角平分线的定义.此题难度适中,注意掌握数形结合思想与整体思想的应用.

练习册系列答案
相关题目
 已知a,b,c在数轴上的位置如图所示,化简|a+c|-|a-2b|-|c-2b|的结果是( )
已知a,b,c在数轴上的位置如图所示,化简|a+c|-|a-2b|-|c-2b|的结果是( )| A、0 | B、4b |
| C、-2a-2c | D、2a-4b |
解方程组
时,一学生把a看错后得到
,而正确的解是
,则a、c、d的值为( )
|
|
|
| A、不能确定 |
| B、a=3、c=1、d=1 |
| C、a=3 c、d不能确定 |
| D、a=3、c=2、d=-2 |
 如图,同心圆的半径为6,8,AB为小圆的弦,CD为大圆的弦,且ABCD为矩形,若矩形ABCD面积最大时,矩形ABCD的周长为
如图,同心圆的半径为6,8,AB为小圆的弦,CD为大圆的弦,且ABCD为矩形,若矩形ABCD面积最大时,矩形ABCD的周长为 如图,在平面直角坐标系中,直线AC与x轴交于点A(4,0),与y轴交于点C(0,4).作OB⊥AC于点B,动点D在边OA上,D(m,0)(0<m<4),过点D作DE⊥OA交折线OB-BA于点E.Rt△GHI的斜边HI在射线AC上,GI∥OA,GI=m,GI与x轴的距离为
如图,在平面直角坐标系中,直线AC与x轴交于点A(4,0),与y轴交于点C(0,4).作OB⊥AC于点B,动点D在边OA上,D(m,0)(0<m<4),过点D作DE⊥OA交折线OB-BA于点E.Rt△GHI的斜边HI在射线AC上,GI∥OA,GI=m,GI与x轴的距离为