Question

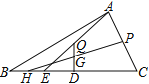
【题目】如图，在△ABC中，D为BC边中点，P为AC边中点，E为BC上一点且BE＝CE，连接AE，取AE中点Q并连接QD，取QD中点G，延长PG与BC边交于点H．若BC＝9，则HE＝_____.

Answer 1

【答案】1．

【解析】

连接PQ．依次求出BE，EC、PQ（用中位线定理）、DH（证明△PQG≌△HDG）、BH即可解决问题．

解：连接PQ．

∵BC＝9，D为BC边中点，BE＝CE，
∴BD=DC=，BE=BC= 2，EC= 7，
∵AQ=QE，AP=PC，

∴PQ∥EC，PQ= EC= ，
∴∠QPG=∠GHD，

∵∠QGP=∠DGH，QG=GD，
∴△PQG≌△HDG（AAS），
∴HD=PQ=，

∴BH=BD-DH=-= 1，
∴HE=BE-BH= 2- 1= 1，
故答案为1．