题目内容
4.在平面直角坐标系中,已知一条直线经过点A(1,1),B(-2,7)和C(a,-3),求a的值.分析 设直线AB解析式为y=kx+b,将A与B坐标代入求出k与b的值,确定出直线AB解析式,代入C坐标即可求得a的值.
解答 解:设直线AB解析式为y=kx+b,
将点A(1,1),B(-2,7)代入得:$\left\{\begin{array}{l}{k+b=1}\\{-2k+b=7}\end{array}\right.$,
解得:k=-2,b=3,
∴直线AB解析式为y=-2x+3,
∵直线AB经过点C(a,-3),
∴-3=-2a+3
∴a=3.
点评 本题考查待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
14.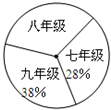 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
请你根据图表中的信息,解答下列问题:
(1)表中的a=2400,b=0.35;请补全扇形统计图;
(2)求该校初中学生平均每人读多少本课外书;
(3)在阋读“科普常识”的5名学生中有3男2女,在这5人中,学校打算随杌选2位进行采访,请你用列表法或树状图法求出所选2位恰妤都为男性的概率.
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.表1是某校初中三个年级学生阅读课外书籍情况统计表,图2是该校初中三个年级学生入数分布扇形统计图,其中八年级人数为408人.| 图书种类 | 频数 | 频率 |
| 科普常识 | 840 | b |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | a | 0.25 |
| 表(1) 其它 | 144 | 0.06 |
(1)表中的a=2400,b=0.35;请补全扇形统计图;
(2)求该校初中学生平均每人读多少本课外书;
(3)在阋读“科普常识”的5名学生中有3男2女,在这5人中,学校打算随杌选2位进行采访,请你用列表法或树状图法求出所选2位恰妤都为男性的概率.
15.下列各对数中,数值相等的数是( )
| A. | 32与23 | B. | -32与(-3)2 | C. | (3×2)3与3×23 | D. | -23与(-2)3 |
13.要时分式$\frac{{x}^{2}-4}{x+2}$有意义,则x应满足的条件为( )
| A. | x≠2 | B. | x≠0 | C. | x≠±2 | D. | x≠-2 |
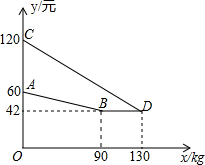 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.