题目内容
如图，抛物线顶点C坐标（1，4），交x轴于点A（3，0），交y轴于点B，则△ABC的面积=________．
3
分析：首先利用顶点式求出二次函数解析式，进而得出图象与y轴交点坐标，即可得出BO的长，进而利用S△ABC=S梯形BOEC+S△CEA-S△BOA分别求出各部分的面积即可．
解答：∵抛物线顶点C坐标（1，4），交x轴于点A（3，0），
∴抛物线的顶点式为：y=a（x-1）2+4，
∴0=a（3-1）2+4，
解得：a=1，
∴y=（x-1）2+4=x2-2x+3，
∴x=0时，
∴y=3，即C点坐标为：（0，3），
S梯形BOEC=
（BO+CE）×EO=（3+4）×1=
，
S△CEA=×CE×AE=×4×（3-1）=4，
S△BOA=×BO×AO=×3×3=
，
∴S△ABC=S梯形BOEC+S△CEA-S△BOA=+4-=3．
故答案为：3．
点评：此题主要考查了顶点式求二次函数解析式，以及三角形与梯形面积求法，根据已知求出各部分面积是解题关键．
分析：首先利用顶点式求出二次函数解析式，进而得出图象与y轴交点坐标，即可得出BO的长，进而利用S△ABC=S梯形BOEC+S△CEA-S△BOA分别求出各部分的面积即可．
解答：∵抛物线顶点C坐标（1，4），交x轴于点A（3，0），
∴抛物线的顶点式为：y=a（x-1）2+4，
∴0=a（3-1）2+4，
解得：a=1，
∴y=（x-1）2+4=x2-2x+3，
∴x=0时，
∴y=3，即C点坐标为：（0，3），
S梯形BOEC=
（BO+CE）×EO=（3+4）×1=，S△CEA=
×CE×AE=×4×（3-1）=4，S△BOA=
×BO×AO=×3×3=，∴S△ABC=S梯形BOEC+S△CEA-S△BOA=
+4-=3．故答案为：3．
点评：此题主要考查了顶点式求二次函数解析式，以及三角形与梯形面积求法，根据已知求出各部分面积是解题关键．
练习册系列答案
相关题目
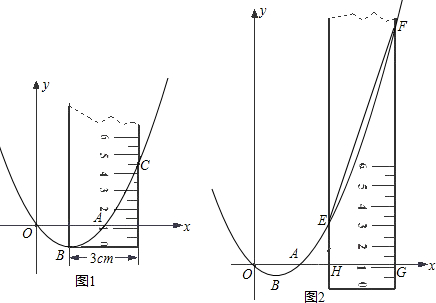
在平面直角坐标系中，将一块腰长为
在平面直角坐标系中，将一块腰长为
cm的等腰直角三角板ABC如图放置，BC边与x轴重合，∠ACB=90°，直角顶点C的坐标为（-3，0）．
