题目内容
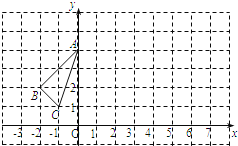
【题目】在平面直角坐标系中，已知点
的坐标为
．将点绕着原点
按逆时针方向旋转
得到点
，延长
到点
，使
；再将点
绕着原点按逆时针方向旋转得到点
，延长
到点
，使
；…如此继续下去．
求：（1）点的坐标；（2）点
的坐标．
【答案】（1）
；（2）
．
【解析】
（1）做P2⊥x轴于一点，利用30°的三角函数可求得P2的横纵坐标；
（2）应先找到各个点所在的象限或者坐标轴的位置．相邻的以奇数开头的两个点在同一直线上，可得到24个点将转一圈：即回到x轴．那么应让2003÷24=83…11可得所求的点在x轴的负半轴上．OP2003的长度应和OP2002的长度相等．∵OP2=21=2；OP4=22=4，∴OP2002=21001，进而可得点P2003的坐标．
设
的坐标为
，作
轴，垂足为
．
∵
．
，
∴
，
，
∴的坐标为；
按照这样的变化规律，点
、
又回到了
轴的正半轴上，
∵
，
∴点
落在轴的负半轴上，
∵
，
，
，…
∴
，
∴点的坐标为．
练习册系列答案
相关题目
