题目内容
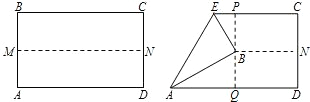
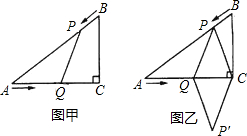
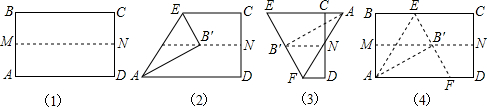
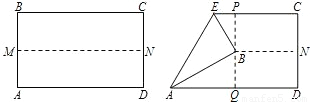
如图,先把一矩形ABCD纸片对折,设折痕为MN,再把点B叠 在折痕线上,得到△ABE.过点B折纸片,使折痕PQ⊥MN于B.
在折痕线上,得到△ABE.过点B折纸片,使折痕PQ⊥MN于B.
(1)求证:△BEP∽△ABQ;
(2)求证:BE2=AE•PE;
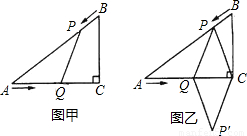
(3)如果沿直线EB折叠纸片,点A是否能叠在直线EC上?请简单说明理由.
(1)证明:∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,
∴∠ABQ=∠PEB.
又∵∠BPE=∠AQB=90°,
∴△PBE∽△QAB.
(2)证明:∵△PBE∽△QAB,
∴ .
.
∵由折叠可知BQ=PB.
∴ ,即
,即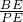 =
= .
.
又∵∠ABE=∠BPE=90°,
∴△PBE∽△BAE,
∴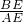 =
=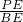 ,
,
即BE2=AE•PE;
(3)解:点A能叠在直线EC上.理由如下:
∵△PBE∽△BAE,
 ∴∠AEB=∠PEB,
∴∠AEB=∠PEB,
则沿EB所在的直线折叠,点A能折叠到直线EC上.
分析:(1)通过证明∠ABQ=∠PEB,∠BPE=∠AQB=90°,得出:△BEP∽△ABQ;
(2)证明 ,即
,即 ,∠ABE=∠BPE=90°,得出△PBE∽△BAE从而问题得证;
,∠ABE=∠BPE=90°,得出△PBE∽△BAE从而问题得证;
(3)由∠AEB=∠CEB可知A能叠在直线EC上.
点评:本题考查了相似三角形的判定和性质.掌握图形的变化中翻折变换(折叠问题)的特点是解决问题的关键.
∴∠ABQ=∠PEB.
又∵∠BPE=∠AQB=90°,
∴△PBE∽△QAB.
(2)证明:∵△PBE∽△QAB,
∴
 .
.∵由折叠可知BQ=PB.
∴
 ,即
,即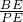 =
= .
.又∵∠ABE=∠BPE=90°,
∴△PBE∽△BAE,
∴
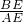 =
=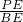 ,
,即BE2=AE•PE;
(3)解:点A能叠在直线EC上.理由如下:
∵△PBE∽△BAE,
 ∴∠AEB=∠PEB,
∴∠AEB=∠PEB,则沿EB所在的直线折叠,点A能折叠到直线EC上.
分析:(1)通过证明∠ABQ=∠PEB,∠BPE=∠AQB=90°,得出:△BEP∽△ABQ;
(2)证明
 ,即
,即 ,∠ABE=∠BPE=90°,得出△PBE∽△BAE从而问题得证;
,∠ABE=∠BPE=90°,得出△PBE∽△BAE从而问题得证;(3)由∠AEB=∠CEB可知A能叠在直线EC上.
点评:本题考查了相似三角形的判定和性质.掌握图形的变化中翻折变换(折叠问题)的特点是解决问题的关键.

练习册系列答案
相关题目