题目内容
关于x的方程x2+bx+1=0与x2-x-b=0有且只有一个公共根,求b的值.
解:设方程的公共根为x=t,
则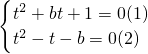 ,
,
由(2)得b=t2-t (3)
将(3)代入(1)得:t3+1=0,
解得,t=-1,
当t=-1时,
b=2.
分析:根据关于x的方程x2+bx+1=0与x2-x-b=0有且只有一个公共根可知,当取该公共根时,可建立方程组,解方程组可得b的值.
点评:本题考查了一元二次方程的解,并熟悉方程和方程组之间的转化.通过此题,体现了转化思想的作用.
则
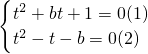 ,
,由(2)得b=t2-t (3)
将(3)代入(1)得:t3+1=0,
解得,t=-1,
当t=-1时,
b=2.
分析:根据关于x的方程x2+bx+1=0与x2-x-b=0有且只有一个公共根可知,当取该公共根时,可建立方程组,解方程组可得b的值.
点评:本题考查了一元二次方程的解,并熟悉方程和方程组之间的转化.通过此题,体现了转化思想的作用.

练习册系列答案
相关题目