题目内容
已知:抛物线y=
(x-1)2-3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
| 3 |
| 4 |
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
(1)抛物线y=
(x-1)2-3,
∵a=
>0,
∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a=
>0,
∴函数y有最小值,最小值为-3;
(3)令x=0,则y=
(0-1)2-3=-
,
所以,点P的坐标为(0,-
),
令y=0,则
(x-1)2-3=0,
解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0),
当点P(0,-
),Q(-1,0)时,设直线PQ的解析式为y=kx+b,
则
,
解得
,
所以直线PQ的解析式为y=-
x-
,
当P(0,-
),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则
,
解得
,
所以,直线PQ的解析式为y=
x-
,
综上所述,直线PQ的解析式为y=-
x-
或y=
x-
.
| 3 |
| 4 |
∵a=
| 3 |
| 4 |
∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a=
| 3 |
| 4 |
∴函数y有最小值,最小值为-3;
(3)令x=0,则y=
| 3 |
| 4 |
| 9 |
| 4 |
所以,点P的坐标为(0,-
| 9 |
| 4 |
令y=0,则
| 3 |
| 4 |
解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0),
当点P(0,-
| 9 |
| 4 |
则
|
解得
|
所以直线PQ的解析式为y=-
| 9 |
| 4 |
| 9 |
| 4 |
当P(0,-
| 9 |
| 4 |
则
|
解得
|
所以,直线PQ的解析式为y=
| 3 |
| 4 |
| 9 |
| 4 |
综上所述,直线PQ的解析式为y=-
| 9 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |

练习册系列答案
相关题目

 如图Rt△ABC中,∠A=90°,tanB=
如图Rt△ABC中,∠A=90°,tanB=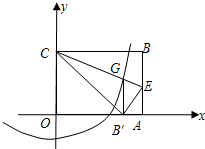 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. (2012•江汉区模拟)已知:抛物线
(2012•江汉区模拟)已知:抛物线