题目内容
如图，已知每个小方格的边长为1，A，B，C三点都在小方格的顶点上，则点C到AB所在直线的距离等于
- A.
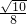
- B.
- C.
- D.
B
分析：连接AB，BC，AC可得△ABC为等腰三角形，根据等腰三角形面积计算方法计算C到AB的距离（过C作AB边上的高）．
解答：
解：连接AB，BC，AC．找到AC中点D，连接BD．设C到AB的距离为h，
小方格边长为1，∴AD=
，AB=BC=，
∴△ABC为等腰三角形，∴BD⊥AC，且BD=
△ABC的面积为S=
AC•BD=4．
又∵△ABC面积=×AB×h=4，
∴h=
=．
故选B．
点评：本题考查了勾股定理的运用，考查了等腰三角形面积的计算，根据面积法求C到AB边的距离h是解题的关键．
分析：连接AB，BC，AC可得△ABC为等腰三角形，根据等腰三角形面积计算方法计算C到AB的距离（过C作AB边上的高）．
解答：
解：连接AB，BC，AC．找到AC中点D，连接BD．设C到AB的距离为h，小方格边长为1，∴AD=
，AB=BC=，∴△ABC为等腰三角形，∴BD⊥AC，且BD=
△ABC的面积为S=
AC•BD=4．又∵△ABC面积=
×AB×h=4，∴h=
=．故选B．
点评：本题考查了勾股定理的运用，考查了等腰三角形面积的计算，根据面积法求C到AB边的距离h是解题的关键．
练习册系列答案
相关题目
如图，已知每个小方格的边长为1，A，B，C三点都在小方格的顶点上，则点C到AB所在直线的距离等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
22、如图，已知每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形．图中的△ABC是一个格点三角形．