题目内容
(12分)如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
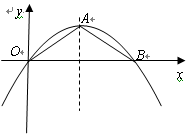
1.(1)求抛物线的解析式;
2.(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
3.(3)连结OA,AB,在x轴下方的抛物线上是否存在点N,使△OBN与△OAB相似?若存在,求出N点的坐标;若不存在,说明理由.
1.(1)由题意,可设抛物线的解析式为![]() ,
,
∵抛物线过原点,
∴ ,
, ![]() .
.
∴抛物线的解析式为![]()
![]() .
.
2.(2)![]() 和所求
和所求![]() 同底不等高,
同底不等高,![]() ,
,
∴ 的高是
的高是![]() 高的3倍,即M点的纵坐标是
高的3倍,即M点的纵坐标是![]() .……………5分
.……………5分
∴ ,即
,即![]() .
.
解之,得 ![]() ,
,![]() .
.
∴满足条件的点有两个: ,
,![]()
3.(3)不存在. …………………………………………………………………………9分
由抛物线的对称性,知![]() ,
,![]() .
.
若![]() 与
与![]() 相似,必有
相似,必有![]() .
.
 设
设![]() 交抛物线的对称轴于
交抛物线的对称轴于![]() 点,显然
点,显然![]() .
.
∴直线![]() 的解析式为
的解析式为![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
∴  .
.
过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .在
.在![]() 中,
中,![]() ,
,![]() ,
,
∴ .
.
又OB=4,
∴ ,
,![]() ,
,![]() 与
与![]() 不相似.
不相似.
同理,在对称轴左边的抛物线上也不存在符合条件的![]() 点.
点.
所以在该抛物线上不存在点N,使![]() 与
与![]() 相似. …………12分
相似. …………12分
解析:略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
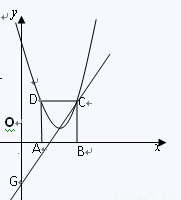
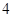 ,
,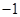 )的抛物线交
)的抛物线交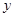 轴于
轴于 点,交
点,交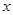 轴于
轴于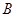 ,
,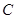 两点(点
两点(点 ,
, ).
).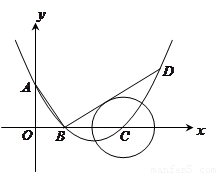
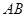 的垂线交抛物线于点
的垂线交抛物线于点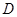 ,
,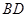 相切,请判断抛物
相切,请判断抛物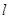 与⊙
与⊙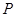 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于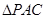 的
的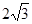 ,直线y=
,直线y=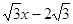 经过点C,交y轴于点G。
经过点C,交y轴于点G。