Question

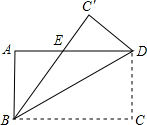
如图，把长方形ABCD沿BD对折，使C点落在C′的位置时，BC′与AD交于E，若AB=6cm，BC=8cm，则重叠部分△BED的面积是（　　）

• A、

  75

  4

• B、

  75

  3

• C、

  75

  2

• D、15

Answer 1

分析：首先根据正方形与折叠的性质，证得△BDE是等腰三角形，然后利用勾股定理与方程思想求得AE的长，则由重叠部分△BED的面积是S_△ABD-S_△ABE，求解即可得到答案．

解答：解：∵四边形ABCD是矩形，
∴∠A=90°，AD=BC=8cm，AD∥BC，
∴∠EDB=∠DBC，
∵长方形ABCD沿BD对折，使C点落在C’的位置时，
∴∠EBD=∠CBD，BC′=BC=8cm，
∴∠EBD=∠EDB，
∴EB=ED，
设AE=xcm，则EB=ED=（8-x）cm，
在Rt△ABE中，
∵AB²+AE²=BE²，
∴36+x²=（8-x）²，
∴x=

7

4

，
∴AE=

7

4

，
∴重叠部分△BED的面积是：S_△ABD-S_△ABE=

1

2

AB•AD-

1

2

AB•AE=

1

2

×6×8-

1

2

×6×

7

4

=

75

4

．
故选A．

点评：此题考查了折叠的性质、正方形的性质以及等腰三角形的判定与性质．解题的关键是数形结合思想的应用．