Question

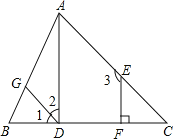
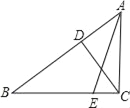
【题目】已知：在△ABC中，∠ACB=90°，CD⊥AB于D，BE：AB=3：5，若CE=，cos∠ACD=．

（1）求cos∠ABC；

（2）AC的值．

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）根据“同角的余角相等”得到，∠ABC=∠ACD，再根据已知cos∠ACD=即可得；

（2）根据，令BC=4k，AB=5k，则AC=3k，由BE：AB=3：5，知BE=3k，从而得CE=k，再根据CE的长即可得．

试题解析：（1）在Rt△ACD与Rt△ABC中，

∵∠ABC+∠CAD=90°，∠ACD+∠CAD=90°，

∴∠ABC=∠ACD，

∴cos∠ABC=cos∠ACD=

（2）在Rt△ABC中， ，令BC=4k，AB=5k，

则AC=3k，

由BE：AB=3：5，

知BE=3k，

则CE=k，且CE=，

则k=，AC=3．