Question

【题目】实验与探究：

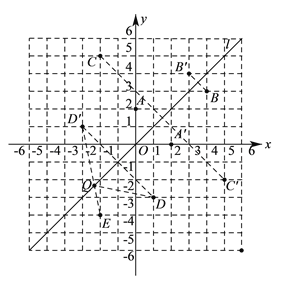
（）如图，直线为第一、三象限的角平分线，观察易知关于直线的对称点的坐标为，请在图中分别标明、关于直线的对称点、的位置，并写出他们的坐标： __________、__________．

（）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为__________ (不必证明)．

（）已知两点、，在直线上是否存在一点，使点到、两点的距离之和最小，并求出最小距离．

Answer 1

【答案】见解析．

【解析】试题分析：（1）根据对称轴为第一、三象限的角平分线，结合图形得出B′、C′两点坐标；（2）由（1）的结论，并与B、C两点坐标进行比较，得出一般规律；（3）由（）得关于直线的对称点的坐标为，连接交直线于点，此时点到、两点距离最小,根据勾股定理求得最短距离即可．

试题解析：

（）

， ．

（）．

（）由（）得关于直线的对称点的坐标为，连接交直线于点，此时点到、两点距离最小．所以存在一点，最小距离为．