题目内容
如图,△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD平分线上一点,EB=EC过点E作EF⊥AC于F,EG⊥AD于G.

(1)请你在不添加辅助线的情况下找出一对你认为全等的三角形,并加以证明;
(2)若AB=3,AC=5,求AF的长.
(1)证明见解析;(2)1.
【解析】
试题分析:已知AE平分∠CAD,EF⊥AC,EG⊥AD及公共边AE,则利用AAS判定△EGA≌△EFA;由△EGA≌△EFA可得到EG=EF,AG=AF,根据HL可判定Rt△EGB≌Rt△EFC,从而得到BG=CF,整理可得到2AF=AC-AB,从而可求得AF的长.
试题解析:(1)△EGA≌△EFA(或△EGB≌△EFC).
证明:∵AE平分∠CAD,
∴∠EAG=∠EAF.
又∵EF⊥AC,EG⊥AD,
∴∠EGA=∠EFA=90°.
在△AEG和△EFA中:
∠EAG=∠EAF,∠EGA=∠EFA,AE=AE,
∴△EGA≌△EFA(AAS).
(2)∵AE平分∠CAD且EF⊥AC,EG⊥AD,
∴EG=EF,∠EGB=∠EFC=90°.
在Rt△EGB和Rt△EFC中
 .
.
∴Rt△EGB≌Rt△EFC(HL).
∴BG=CF.
又∵BG=AB+AG,CF=AC-AF,
即AB+AG=AC-AF,
又∵△EGA≌△EFA,
∴AG=AF.
∴2AF=AC-AB=5-3=2.
∴AF=1.
考点:全等三角形的判定与性质.

练习册系列答案
相关题目


 A.
A. B.
B. C.
C. D.
D.
 ,-
,- ,(-2)3 ,-24这四个数中,负数共有 ( )
,(-2)3 ,-24这四个数中,负数共有 ( ) = .
= . )•
)• ,其中a=3.
,其中a=3.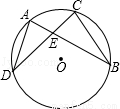
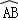 与
与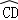 的长度,并证明你的结论;
的长度,并证明你的结论;