��Ŀ����
����Ŀ���ۺ���ʵ��
�����������������������̽��
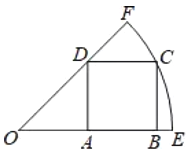
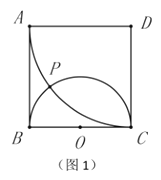
���壺��ͼ1����������![]() �У���
�У���![]() Ϊֱ������Բ
Ϊֱ������Բ![]() ����
����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��
Ϊ�뾶��![]() �����Բ
�����Բ![]() ���ڵ�
���ڵ�![]() .���dzƵ�
.���dzƵ�![]() Ϊ������
Ϊ������![]() ��һ��������������������Ķ����߶���������
��һ��������������������Ķ����߶���������![]() ������λ�ù�ϵ����������ϵ�������в�������������ֵ��̽����
������λ�ù�ϵ����������ϵ�������в�������������ֵ��̽����
����̽������ͼ2������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ��Բ
Ϊ��Բ![]() �����ߣ�
�����ߣ�
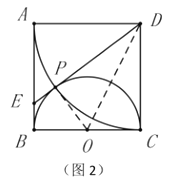
֤��������![]() ��
��
����ͼ��֪��![]() ��
��
��![]() ��
��
![]()
![]() ����
����![]() �ǰ�Բ
�ǰ�Բ![]() �����ߣ�
�����ߣ�
��������
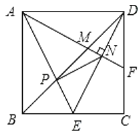
��1����ͼ3����ͼ2�Ļ����ϣ�����![]() .���ж�
.���ж�![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
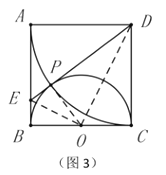
��2���ڣ�1���������£���ֱ��д���߶�![]() ֮���������ϵ��
֮���������ϵ��
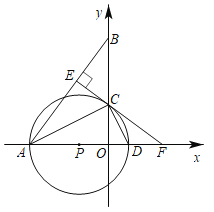
��3����ͼ4����֪��![]() Ϊ������
Ϊ������![]() ��һ���������������
��һ���������������![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����д��
�����![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
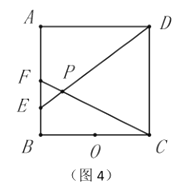
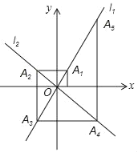
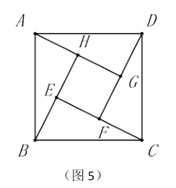
��4����ͼ5����֪��![]() Ϊ������
Ϊ������![]() ���ĸ����������������
���ĸ����������������![]() ��ǡ�õõ�һ�����������ˬ��ͼ���������ͼ�Σ�̽����ֱ��д��һ����ȫ�ȵļ���ͼ�����֮���������ϵ��
��ǡ�õõ�һ�����������ˬ��ͼ���������ͼ�Σ�̽����ֱ��д��һ����ȫ�ȵļ���ͼ�����֮���������ϵ��
���𰸡���1��![]() �����ɼ���������2��
�����ɼ���������2��![]() ����3��
����3��![]() �����ɼ���������4���𰸲�Ψһ���磺
�����ɼ���������4���𰸲�Ψһ���磺![]() ���������������
���������������![]() �������������
�������������![]() ���������������
���������������![]() �����
�����![]() �ȣ�
�ȣ�
��������
��1����������룬��ͼ2�Լ�������۵Ļ����ϣ�����ȫ�������ε����ʡ��ı��ε��ڽǺ͡��ڲ��ǵ����ʿɵó�![]() �����ɱ߱߱߶�����֤��
�����ɱ߱߱߶�����֤��![]() ��Ȼ������ȫ�������ε����ʡ���ʽ���ʿɵ�֤���ۣ�
��Ȼ������ȫ�������ε����ʡ���ʽ���ʿɵ�֤���ۣ�
��2���ɣ�1����֪![]() ��
��![]() ������ȫ�������ε����ʡ��߶εĺͲ�ɵõ����ۣ�
������ȫ�������ε����ʡ��߶εĺͲ�ɵõ����ۣ�
��3����������룬���Ӹ����߹����ֱ�������Σ��ɣ�1����֪![]() ����������ֵ��ȣ��ٸ��������ε����ʼ��ɵ�֤���ۣ�
����������ֵ��ȣ��ٸ��������ε����ʼ��ɵ�֤���ۣ�
��4������ǰ��Ľ��۽����ˬ��ͼ��֤��
![]() ������������룮
������������룮
�⣺��1�����ۣ�![]()
�������£�
��![]()
��![]() ��
��![]() ��
��![]()
��![]()
��![]()
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]()
��![]()
��![]()
��![]()
��![]() ��
��
��2�����ɣ�1����֪��![]() ��
��![]()
��![]() ��
��![]()
��![]()
��![]()
���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��![]() ��
��
��3�����ۣ�![]()
���ɣ�����![]() ��
��![]() ����ͼ��
����ͼ��
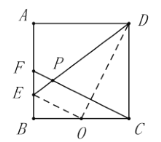
�ɣ�1����֪��![]()
��![]()
��![]()
�ߵ�![]() Ϊ
Ϊ![]() ���е�
���е�
��![]()
��![]()
���ı���![]() ��������
��������
��![]()
��![]() ��
��
��4���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����ͼ��
����ͼ��
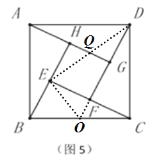
����ǰ��Ľ��ۿ�֪![]()
��![]()
�ߴ�ͼΪ��ˬ��ͼ��![]()
��![]()
ͬ���ɵ�![]() ��
��![]() ��
��![]()
���ı���![]() ��������
��������
��![]()
��![]()
����![]() ��
��![]() ��
�У�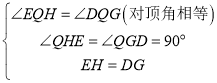
��![]()
��![]()
��![]()
��![]()
��𰸲�Ψһ�����磬![]() ���������������
���������������![]() �������������
�������������![]() ���������������
���������������![]() �����
�����![]() �ȵȣ�
�ȵȣ�