题目内容
 如图:直线y=x-4与坐标轴交于A、B,与双曲线
如图:直线y=x-4与坐标轴交于A、B,与双曲线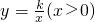 交于C、D,BE=2BD,EF⊥y轴于F,若S△BEF+S△OBD=4,则k=________.
交于C、D,BE=2BD,EF⊥y轴于F,若S△BEF+S△OBD=4,则k=________.
-3
分析:根据直线y=x-4与坐标轴交于A、B,可以得出A,B两点坐标,再证明△DGB∽△EFB,利用的面积和为4列出方程,进而求出即可.
解答: 解:过D作DG垂直于y轴于G,
解:过D作DG垂直于y轴于G,
∵直线y=x-4与坐标轴交于A、B,
∴A(4,0),B(-4,0),
如果设点D坐标为(m,n),则D点在反比例函数图象上,有mn=k ①,
D点在直线上,有n=m-4 ②,
GD=m,OG=-n,BG=4-OG=4+n,
∵∠GBD=∠EBF,
∠DGB=∠BFE,
∴△DGB∽△EFB,
∵ =
= =
= =
= ,
,
∴BF=2BG,则BF=2BG=8+2n,EF=2GD=2m,
∵S△BEF+S△OBD=4,
∴OB×GD+BF×EF=2×4,
∴4m+(8+2n)×2m=8,
∵n=m-4,
∴整理得出:m2+m-2=0,
∴(m-1)(m+2)=0.
∴m1=1,m2=-2(不合题意舍去),
∴n=1-4=-3,
∴D点坐标为:(1,-3),
∴k=1×(-3)=-3.
故答案为:-3.
点评:此题主要考查了反比例函数的综合应用以及一次函数有关性质应用,根据已知D点坐标得出BF=2BG,则BF=2BG=8+2n,EF=2GD=2m是解题关键.
分析:根据直线y=x-4与坐标轴交于A、B,可以得出A,B两点坐标,再证明△DGB∽△EFB,利用的面积和为4列出方程,进而求出即可.
解答:
 解:过D作DG垂直于y轴于G,
解:过D作DG垂直于y轴于G,∵直线y=x-4与坐标轴交于A、B,
∴A(4,0),B(-4,0),
如果设点D坐标为(m,n),则D点在反比例函数图象上,有mn=k ①,
D点在直线上,有n=m-4 ②,
GD=m,OG=-n,BG=4-OG=4+n,
∵∠GBD=∠EBF,
∠DGB=∠BFE,
∴△DGB∽△EFB,
∵
 =
= =
= =
= ,
,∴BF=2BG,则BF=2BG=8+2n,EF=2GD=2m,
∵S△BEF+S△OBD=4,
∴OB×GD+BF×EF=2×4,
∴4m+(8+2n)×2m=8,
∵n=m-4,
∴整理得出:m2+m-2=0,
∴(m-1)(m+2)=0.
∴m1=1,m2=-2(不合题意舍去),
∴n=1-4=-3,
∴D点坐标为:(1,-3),
∴k=1×(-3)=-3.
故答案为:-3.
点评:此题主要考查了反比例函数的综合应用以及一次函数有关性质应用,根据已知D点坐标得出BF=2BG,则BF=2BG=8+2n,EF=2GD=2m是解题关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目

 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( ) 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数 17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).
17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).