Question

如图，点E、F、G是双曲线y=

k

x

上的点，过E、F、G分别作EB、FC、GD垂直于x轴，垂足分别为B、C、D，且OB=BC=CD，△OBE的面积记为S₁，△BCF的面积记为S₂，△CDG的面积记为S₃，若S₁+S₃=2，则S₂=

3

4

．

Answer 1

分析：连OF、OG，根据反比例y=

k

x

（k≠0）数k的几何意义得到S₁=△OCF的面积=△OGD的面积=k，而OB=BC=CD，得到△OCF的面积=2S₂，△OGD的面积=3S₃，利用S₁+S₃=2可求出k的值，然后根据S₂=

1

2

k进行计算即可．

解答：解：连OF、OG，如图，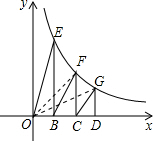
∵S₁=△OCF的面积=△OGD的面积=k，
∵OB=BC=CD，
∴△OCF的面积=2S₂，△OGD的面积=3S₃，
即S₂=

1

2

k，S₃=

1

3

k，
∴k+

1

3

k=2，
∴k=

3

2

，
∴S₂=

1

2

k=

1

2

×

3

2

=

3

4

．
故答案为

3

4

．

点评：本题考查了反比例y=

k

x

（k≠0）数k的几何意义：过反比例函数图象上任意一点分别作x轴、y轴的垂线，则垂线与坐标轴所围成的矩形的面积为|k|．也考查了三角形面积公式．