题目内容
解答下列问题(1)已知a=
| 2 |
| 2 |
(2)已知x=2-
| 3 |
| 3 |
(3)己知x=
| 2 |
| x |
| x-2 |
| 4 |
| 2-x |
分析:将代数式化简后将已知未知数的值代入求得即可.
解答:解:(1)a2+ab+b2,
=a2+2ab+b2-ab,
=(a+b)2-ab,
当a=
+1,b=
-1时,
原式=(
+1+
-1)2-(
+1)(
-1),
=8-1,
=7;
(2)x2-xy+y2,
=x2-2xy+y2-xy,
=(x-y)2-xy
当x=2-
,y=2+
时,
原式=(2+
-2+
)2-(2-
)(2+
),
=16-1,
=15;
(3)
÷(2+x-
),
=
÷
,
=
×
,
=
当x=
-1时,原式=
,
=
+1.
=a2+2ab+b2-ab,
=(a+b)2-ab,
当a=
| 2 |
| 2 |
原式=(
| 2 |
| 2 |
| 2 |
| 2 |
=8-1,
=7;
(2)x2-xy+y2,
=x2-2xy+y2-xy,
=(x-y)2-xy
当x=2-
| 3 |
| 3 |
原式=(2+
| 3 |
| 3 |
| 3 |
| 3 |
=16-1,
=15;
(3)
| x |
| x-2 |
| 4 |
| 2-x |
=
| x |
| x-2 |
| -x2 |
| 2-x |
=
| x |
| x-2 |
| x-2 |
| x2 |
=
| 1 |
| x |
当x=
| 2 |
| 1 | ||
|
=
| 2 |
点评:本题考查了代数式的基本变形及二次根式的化简的知识,具有一定的挑战性.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

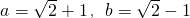 ,求a2+ab+b2的值.
,求a2+ab+b2的值.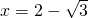 ,
, ,求x2-xy+y2的值.
,求x2-xy+y2的值.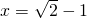 ,化简求代数式
,化简求代数式 的值.
的值. ,求a2+ab+b2的值.
,求a2+ab+b2的值. ,
, ,求x2-xy+y2的值.
,求x2-xy+y2的值. ,化简求代数式
,化简求代数式 的值.
的值.