Question

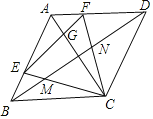
【题目】如图，已知边长为4的菱形ABCD中，AC＝BC，E，F分别为AB，AD边上的动点，满足BE＝AF，连接EF交AC于点G，CE、CF分别交BD与点M，N，给出下列结论：①∠AFC＝∠AGE；②EF＝BE+DF；③△ECF面积的最小值为3，④若AF＝2，则BM＝MN＝DN；⑤若AF＝1，则EF＝3FG；其中所有正确结论的序号是_____．

Answer 1

【答案】①③④

【解析】

由“SAS”可证△BEC≌△AFC，再证△EFC是等边三角形，由外角的性质可证∠AFC=∠AGE；由点E在AB上运动，可得BE+DF≥EF；由等边三角形的性质可得△ECF面积的EC2，则当EC⊥AB时，△ECF的最小值为3；由等边三角形的性质和菱形的性质可求MN＝BD﹣BM﹣DN＝，由平行线分线段成比例可求EG=3FG，即可求解．

∵四边形ABCD是菱形，

∴AB＝BC＝CD＝AD＝4，

∵AC＝BC，

∴AB＝BC＝CD＝AD＝AC，

∴△ABC，△ACD是等边三角形，

∴∠ABC＝∠BAC＝∠ACB＝∠DAC＝60°，

∵AC＝BC，∠ABC＝∠DAC，AF＝BE，

∴△BEC≌△AFC（SAS）

∴CF＝CE，∠BCE＝∠ACF，

∴∠ECF＝∠BCA＝60°，

∴△EFC是等边三角形，

∴∠EFC＝60°，

∵∠AFC＝∠AFE+∠EFC＝60°+∠AFE，∠AGE＝∠AFE+∠CAD＝60°+∠AFE，

∴∠AFC＝∠AGE，故①正确；

∵BE+DF＝AF+DF＝AD，EF＝CF≤AC，

∴BE+DF≥EF（当点E与点B重合时，BE+DF＝EF），

故②不正确；

∵△ECF是等边三角形，

∴△ECF面积的EC2，

∴当EC⊥AB时，△ECF面积有最小值，

此时，EC＝2，△ECF面积的最小值为3，故③正确；

如图，设AC与BD的交点为O，

若AF＝2，则FD＝BE＝AE＝2，

∴点E为AB中点，点F为AD中点，

∵四边形ABCD是菱形，

∴AC⊥BD，AO＝CO，BO＝DO，∠ABO＝∠ABC＝30°，

∴AO＝AB＝2，BO＝AO＝2，

∴BD＝4，

∵△ABC是等边三角形，BE＝AE＝2，

∴CE⊥AB，且∠ABO＝30°，

∴BE＝EM＝2，BM＝2EM，

∴BM＝，

同理可得DN＝，

∴MN＝BD﹣BM﹣DN＝，

∴BM＝MN＝DN，故④正确；

如图，过点E作EH∥AD，交AC于H，

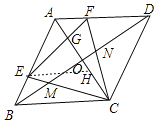
∵AF＝BE＝1，

∴AE＝3，

∵EH∥AD∥BC，

∴∠AEH＝∠ABC＝60°，∠AHE＝∠ACB＝60°，

∴△AEH是等边三角形，

∴EH＝AE＝3，

∵AD∥EH，

∴，

∴EG＝3FG，故⑤错误，

故答案为：①③④