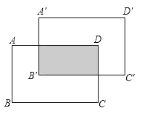
��Ŀ����
����Ŀ����ͼ��AD����O��ֱ����AD=12����B��C����O�ϣ�AB��DC���ӳ��߽��ڵ�E����CB=CE����BCE=70��.

�����½��ۣ��١�ADE=��E�����ӻ�![]() �ij�Ϊ
�ij�Ϊ![]() ���۵�CΪ
���۵�CΪ![]() ���е㣻��BDƽ�֡�ADE.���Ͻ���һ����ȷ����_________________.������ȷ���۵���Ŷ����ϣ�
���е㣻��BDƽ�֡�ADE.���Ͻ���һ����ȷ����_________________.������ȷ���۵���Ŷ����ϣ�
���𰸡��٢ڢ�
���������������ٸ����ڽ��ı��εĶԽǻ����õ���CBE=��ADE�����ݵ��������ε����ʵõ���CBE=��E������֤��.
�����Բ�ĽǵĶ��������ݻ�����ʽ��⼴��.
��֤����DAC=��EAC������֤��.
�ܡ�A����E��BD��ƽ�֡�ADE.
��⣺�١�CBEΪԲ�ڽ��ı���ABCD����ǣ����CBE=��ADE��
CB=CE�����ԡ�CBE=��E����ˡ�ADE=��E.
�ڡ�A=��BCE=70�㣬���AOB=40�㣬![]() �ij�=
�ij�=![]()
��������֪��AC��DE���ɡ�ADE=��E��AD=AE��
���DAC=��EAC�����CΪ![]() ���е�.
���е�.
��DB��AE������A����E����BD��ƽ�֡�ADE. ��ȷ���ۢ٢ڢ�
�ʴ�Ϊ���٢ڢ�.
�㾦������Բ���ۺ��⣬����Բ�ڽ��ı��ε����ʣ�Բ�ܽǶ�����������ʽ�ȣ�����֪ʶ��϶࣬��ѧ���ۺϷ�������Ҫ��ϸ�.
�����͡������
��������
15
����Ŀ�����㣺![]() .
.
���𰸡�1
������������������ʵ��������˳��������㼴��.
��⣺ԭʽ![]()
![]()
![]()

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�����Ŀ���±���ijˮ��վ���꼾��ij����һ����ˮλ�仯����ļ�¼������Ϊ�����½�Ϊ����
ʱ�� | ����һ | ���ڶ� | ������ | ������ | ������ | ������ | ������ |
ˮλ�仯/ | +0.2 | +0.3 | -0.4 | -0.4 | -0.1 | +0.2 | +0.4 |
ע���ٱ��м�¼������Ϊÿ������12ʱ��ˮλ��ǰһ��12ʱˮλ�ı仯��������������12ʱ��ˮλ�߶�Ϊ![]() .
.

��1������ͨ������˵������������������ȣ�ˮλ�������˻����½��ˣ�
��2�����������ӱ���ÿ���ˮλ������������˵��ˮλ�ڱ����ڵ���������.