Question

【题目】如图，在平面直角坐标系中，等腰△OBC的边OB在x轴上，OB=CB，OB边上的高CA与OC边上的高BE相交于点D，连接OD，AB=，∠CBO=45°，在直线BE上求点M，使△BMC与△ODC相似，则点M的坐标是 ．

Answer 1

【答案】（1，）或（ ， ）
【解析】解：∵OB=CB，OB边上的高CA与OC边上的高BE相交于点D，AB=，∠CBO=45°，
∴AB=AC=，OD=CD，∠BOC==67.5°，
在Rt△BAC中，BC==2，
∴OB=2，
∴OA=OB﹣AB=2﹣，
在Rt△OAC中，OC==2，
在Rt△OAD中，OA2+AD2=OD2 ，
（2﹣）2+AD2=（﹣AD）2 ，
解得：AD=2﹣，
∴OA=AD，∠DOA=45°，
∴OD=CD=2﹣2，
在Rt△BAD中，BD==2，
①如图1，△BMC∽△CDO时，过M点作MF⊥AB于F，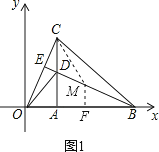

=，即=，
解得BM=，
∵MF⊥AB，CA是OB边上的高，
∴MF∥DA，
∴△BMF∽△BDA，
∴，即==，
解得BF=1，MF=﹣1，
∴OF=OB﹣BF=1，
∴点M的坐标是（1，﹣1）；
②如图2，△BCM∽△CDO时，过M点作MF⊥AB于F，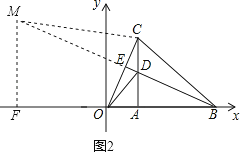

，即=，
解得BM=2，
∵MF⊥AB，CA是OB边上的高，
∴MF∥DA，
∴△BMF∽△BDA，
∴ ， 即==，
解得BF=2+，MF=，
∴OF=BF﹣OB=，
∴点M的坐标是（﹣，）．
综上所述，点M的坐标是（1，﹣1）或（﹣，）．
所以答案是：（1，﹣1）或（﹣，）．
【考点精析】通过灵活运用一次函数的图象和性质和相似三角形的判定与性质，掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．