题目内容
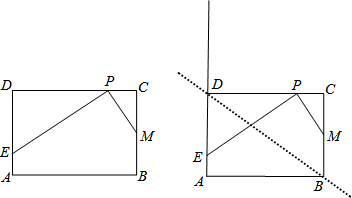
 已知:在矩形ABCD中,对角线AC,BD相交于O,AC=2AD,过点B作BE∥AC交DA的延长线于点E,试判断△BDE的形状.
已知:在矩形ABCD中,对角线AC,BD相交于O,AC=2AD,过点B作BE∥AC交DA的延长线于点E,试判断△BDE的形状.
解:△BDE是等边三角形.
理由:∵四边形ABCD是矩形,
∴BD=AC,AD∥BC,AC=2OA,BD=2OD,
∵AC=2AD,
∴OA=OD=AD,
∴△OAD是等边三角形,
∴∠ADO=60°,
∵BE∥AC,
∴四边形AEBC是平行四边形,
∴BE=AC,
∴BD=BE,
∴△BDE是等边三角形.
分析:由在矩形ABCD中,对角线AC,BD相交于O,AC=2AD,易得△OAD是等边三角形,则可得∠ADO=60°,又由BE∥AC,可证得四边形AEBC是平行四边形,继而可得BD=BE,则可证得△BDE是等边三角形.
点评:此题考查了矩形的性质、平行四边形以及等边三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.
理由:∵四边形ABCD是矩形,
∴BD=AC,AD∥BC,AC=2OA,BD=2OD,
∵AC=2AD,
∴OA=OD=AD,
∴△OAD是等边三角形,
∴∠ADO=60°,
∵BE∥AC,
∴四边形AEBC是平行四边形,
∴BE=AC,
∴BD=BE,
∴△BDE是等边三角形.
分析:由在矩形ABCD中,对角线AC,BD相交于O,AC=2AD,易得△OAD是等边三角形,则可得∠ADO=60°,又由BE∥AC,可证得四边形AEBC是平行四边形,继而可得BD=BE,则可证得△BDE是等边三角形.
点评:此题考查了矩形的性质、平行四边形以及等边三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目