��Ŀ����
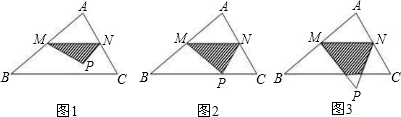
��ͼ1���ڡ�ABC�У���A=90�㣬AB=4��AC=3��M�DZ�AB�ϵĶ��㣨M����A��B�غϣ���MN��BC��AC�ڵ�N����AMN����MN�ĶԳ�ͼ���ǡ�PMN����AM=x��
��1���ú�x��ʽ�ӱ�ʾ��AMN�����������д�����̣���
��2����xΪ��ֵʱ����Pǡ�����ڱ�BC�ϣ�
��3���ڶ���M���˶������У��ǡ�PMN������MBCN�ص����ֵ����Ϊy������y����x�ĺ�����ϵʽ������xΪ��ֵʱ���ص����ֵ��������������Ƕ��٣�
��1���ú�x��ʽ�ӱ�ʾ��AMN�����������д�����̣���
��2����xΪ��ֵʱ����Pǡ�����ڱ�BC�ϣ�
��3���ڶ���M���˶������У��ǡ�PMN������MBCN�ص����ֵ����Ϊy������y����x�ĺ�����ϵʽ������xΪ��ֵʱ���ص����ֵ��������������Ƕ��٣�

��1��S��AMN=
x2��3����
��2����ͼ2������Գ�����֪��AM=PM����AMN=��PMN����4�֣�
��MN��BC�����PMN=��BPM����AMN=��B����5��
���B=��BPM��AM=PM=BM��6�֣�
���M��AB�е㣬����x=
AB=2ʱ����Pǡ�����ڱ�BC�ϣ���7�֣�
��3����i�����·�����������ۣ�
�ٵ�0��x��2ʱ����y=
x2��8�֣�
�ڵ�2��x��4ʱ����ͼ3����PM��PN�ֱ�BC��E��F
�ɣ�2��֪ME=MB=4-x��
��PE=PM-ME=x-��4-x��=2x-4
������֪��PEF����ABC��
��(
)2=
��
��S��PEF=
(x-2)2
��y=S��PMN-S��PEF=
x2-
(x-2)2=-
x2+6x-6
��y=
��ii���ߵ�0��x��2ʱ��y=
x2
����֪y���=
��22=
��11�֣�
�֡ߵ�2��x��4ʱ��y=-
x2+6x-6=-
��x-
��2+2��
�൱x=
ʱ������2��x��4����y���=2����12�֣�
������������x=
ʱ���ص����ֵ���������ֵΪ2����13�֣�

| 3 |
| 8 |
��2����ͼ2������Գ�����֪��AM=PM����AMN=��PMN����4�֣�
��MN��BC�����PMN=��BPM����AMN=��B����5��
���B=��BPM��AM=PM=BM��6�֣�
���M��AB�е㣬����x=
| 1 |
| 2 |
��3����i�����·�����������ۣ�
�ٵ�0��x��2ʱ����y=
| 3 |
| 8 |
�ڵ�2��x��4ʱ����ͼ3����PM��PN�ֱ�BC��E��F
�ɣ�2��֪ME=MB=4-x��
��PE=PM-ME=x-��4-x��=2x-4
������֪��PEF����ABC��
��(
| PE |
| AB |
| S��PEF |
| S��ABC |
��S��PEF=
| 3 |
| 2 |
��y=S��PMN-S��PEF=
| 3 |
| 8 |
| 3 |
| 2 |
| 9 |
| 8 |
��y=
|
��ii���ߵ�0��x��2ʱ��y=
| 3 |
| 8 |
����֪y���=
| 3 |
| 8 |
| 3 |
| 2 |
�֡ߵ�2��x��4ʱ��y=-
| 9 |
| 8 |
| 9 |
| 8 |
| 8 |
| 3 |
�൱x=
| 8 |
| 3 |
������������x=
| 8 |
| 3 |


��ϰ��ϵ�д�
�����Ŀ

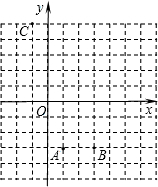

 ��ȵ������֣���P������꣮
��ȵ������֣���P������꣮
 ��ʼ���߶�OA����ÿ��1����λ���ȵ��ٶ����A�ƶ�����P��Q�ƶ���ʱ��Ϊt�룮
��ʼ���߶�OA����ÿ��1����λ���ȵ��ٶ����A�ƶ�����P��Q�ƶ���ʱ��Ϊt�룮