题目内容
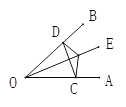
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连接CD,过点B作BG丄CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:
①![]() ; ②点F是GE的中点; ③AF=
; ②点F是GE的中点; ③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.
AB;④S△ABC=5S△BDF,其中正确的结论序号是__________.

【答案】①③
【解析】试题分析:∵在Rt△ABC中,∠ABC=90°,∴AB⊥BC,AG⊥AB,∴AG∥BC,∴△AFG∽△CFB,
∴![]() ,∵BA=BC,∴
,∵BA=BC,∴![]() ,故①正确;∵∠ABC=90°,BG⊥CD∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
,故①正确;∵∠ABC=90°,BG⊥CD∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
∴∠DBE=∠BCD,∵AB=CB,点D是AB的中点,∴BD=![]() AB=
AB=![]() CB,∵tan∠BCD=
CB,∵tan∠BCD=![]() =
=![]() ,∴在Rt△ABG中,tan∠DBE=
,∴在Rt△ABG中,tan∠DBE=![]() =
=![]() ,∵
,∵![]() ,∴FG=
,∴FG=![]() FB,故②错误;∵△AFG∽△CFB,∴AF:CF=AG:BC=1:2,
FB,故②错误;∵△AFG∽△CFB,∴AF:CF=AG:BC=1:2,
∴AF=![]() AC,∵AC=
AC,∵AC=![]() AB,∴AF=
AB,∴AF=![]() AB,故③正确;∵BD=
AB,故③正确;∵BD=![]() AB,AF=
AB,AF=![]() AC,∴S△ABC=6S△BDF,故④错误.故答案为:①③.
AC,∴S△ABC=6S△BDF,故④错误.故答案为:①③.

练习册系列答案
相关题目