题目内容
世界杯期间，为了让广大球迷尽情享受足球的乐趣又不影响家人的正常休息，我市某大型酒店提供了“世界杯专用包房”服务．该酒店共有包房100间，每晚每间包房收包房费100元时，所有包房便都可租出；若每间包房的收费每提高50元，所租出的包房就会减少10间，依此类推．设每间包房收费提高x（元），每晚包房费的总收入为y（元），则y与x的关系式为________．
y=-
x2+80x+10000
分析：由题知每间的包房的收费为100元，每次都是在这个基础上增加的，所以提高x元后每间包房的收入为（100+x）元；又由每提高50元，所租出的包房就会减少10间，所以提高x元后，包房可租出（100-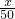
×10）间，进而得出y与x的关系式．
解答：∵每间的包房价格是在100元的基础上增加的，
∴收费提高x元后，每间包房的收入为（100+x）元，
∵每提高20元，包房少10间，
∴可租出（100-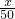×10）间，
故y与x的关系式为：y=（100+x）（100-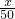×10）=-x2+80x+10000；
故答案为：y=-x2+80x+10000．
点评：本题考查了函数关系式的求法，升降价问题是考试重点，同学们应重点掌握．
x2+80x+10000分析：由题知每间的包房的收费为100元，每次都是在这个基础上增加的，所以提高x元后每间包房的收入为（100+x）元；又由每提高50元，所租出的包房就会减少10间，所以提高x元后，包房可租出（100-
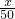×10）间，进而得出y与x的关系式．解答：∵每间的包房价格是在100元的基础上增加的，
∴收费提高x元后，每间包房的收入为（100+x）元，
∵每提高20元，包房少10间，
∴可租出（100-
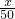×10）间，故y与x的关系式为：y=（100+x）（100-
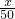×10）=-x2+80x+10000；故答案为：y=-
x2+80x+10000．点评：本题考查了函数关系式的求法，升降价问题是考试重点，同学们应重点掌握．
练习册系列答案
相关题目
“五一”期间，为了满足广大人民的消费需求，某商店计划用160000元购进一批家电，这批家电的进价和售价如下表：
（1）若全部资金用来购买彩电和洗衣机共100台，问商店可以购买彩电和洗衣机各多少台？
（2）若在现有资金160000元允许的范围内，购买上表中三类家电共100台，其中彩电台数和冰箱台数相同，且购买洗衣机的台数不超过购买彩电的台数，请你算一算有几种进货方案？哪种进货方案能使商店销售完这批家电后获得的利润最大？并求出最大利润．（利润=售价-进价）
| 类别 | 彩电 | 冰箱 | 洗衣机 |
| 进价 | 2000 | 1600 | 1000 |
| 售价 | 2200 | 1800 | 1100 |
（2）若在现有资金160000元允许的范围内，购买上表中三类家电共100台，其中彩电台数和冰箱台数相同，且购买洗衣机的台数不超过购买彩电的台数，请你算一算有几种进货方案？哪种进货方案能使商店销售完这批家电后获得的利润最大？并求出最大利润．（利润=售价-进价）