题目内容
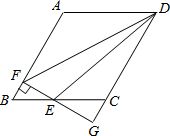 如图,?ABCD中,AB=4,BC=3,∠BAD=120°,动点E在BC上(不与B重合).作EF⊥AB于F,FE、DC的延长线交于点G.设BE=x,△DEF的面积为S.
如图,?ABCD中,AB=4,BC=3,∠BAD=120°,动点E在BC上(不与B重合).作EF⊥AB于F,FE、DC的延长线交于点G.设BE=x,△DEF的面积为S.
(1)求S关于x的函数表达式,并写出x的取值范围;
(2)当点E在何处时,S有最大值,最大值为多少?
解:(1)在?ABCD中,AB∥CD,
∵EF⊥AB,
∴EF⊥DC,
∴DG为△DEF边EF上的高,
在Rt△BFE中,∠B=180°-∠BAD=180°-120°=60°,
EF=BEsinB= x,
x,
在Rt△CEG中,CE=3-x,CG=(3-x)cos60°= ,
,
∴DG=DC+CG=4+ =
= ,
,
∴S= EF•DG=
EF•DG= ×
× x×
x× =-
=- x2+
x2+ x,
x,
其中0<x≤3;
(2)∵a=- <0,对称轴为x=-
<0,对称轴为x=- =-
=-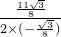 =
= ,
,
∴当0<x≤3时,S随x的增大而增大,
∴当x=3,即E与C重合时,S有最大值,
S最大=- ×9+
×9+ ×3=3
×3=3 .
.
分析:(1)根据平行四边形的对边平行判断出DG是△DEF的EF边上的高,再根据平行四边形的邻角互补求出∠B=60°,然后解直角三角形求出EF的长,用x表示出CE,解直角三角形求出CG再根据平行四边形对边相等可得CD=AB=4,然后表示出DG,根据三角形的面积公式列式整理即可得解;
(2)根据二次函数的最值问题以及增减性解答.
点评:本题考查了平行四边形的对边平行的性质,解直角三角形,三角形的面积公式,利用二次函数的增减性求函数的最值,综合题,但难度不大.
∵EF⊥AB,
∴EF⊥DC,
∴DG为△DEF边EF上的高,
在Rt△BFE中,∠B=180°-∠BAD=180°-120°=60°,
EF=BEsinB=
 x,
x,在Rt△CEG中,CE=3-x,CG=(3-x)cos60°=
 ,
,∴DG=DC+CG=4+
 =
= ,
,∴S=
 EF•DG=
EF•DG= ×
× x×
x× =-
=- x2+
x2+ x,
x,其中0<x≤3;
(2)∵a=-
 <0,对称轴为x=-
<0,对称轴为x=- =-
=-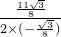 =
= ,
,∴当0<x≤3时,S随x的增大而增大,
∴当x=3,即E与C重合时,S有最大值,
S最大=-
 ×9+
×9+ ×3=3
×3=3 .
.分析:(1)根据平行四边形的对边平行判断出DG是△DEF的EF边上的高,再根据平行四边形的邻角互补求出∠B=60°,然后解直角三角形求出EF的长,用x表示出CE,解直角三角形求出CG再根据平行四边形对边相等可得CD=AB=4,然后表示出DG,根据三角形的面积公式列式整理即可得解;
(2)根据二次函数的最值问题以及增减性解答.
点评:本题考查了平行四边形的对边平行的性质,解直角三角形,三角形的面积公式,利用二次函数的增减性求函数的最值,综合题,但难度不大.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
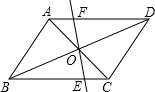
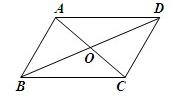 9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )
9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )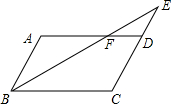 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=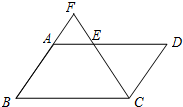 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F. (1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为
(1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为