题目内容
 如图,在等腰直角△ABC中,CA=CB=3,D是BC上一点,且
如图,在等腰直角△ABC中,CA=CB=3,D是BC上一点,且| CD |
| AD |
| 1 |
| 2 |
A、1+
| ||
B、1+
| ||
C、1+2
| ||
D、1+
|
分析:先根据△ABC是等腰直角三角形得出∠BAC的度数,由CA=CB=3,D是BC上一点,且
=
求出AD的长,作点D关于直线AB的对称点D′,连接CD′,由线段垂直平分线的性质可知,AD=AD′,∠DAD′=2∠BAC=90°,在Rt△ACD′中根据勾股定理即可求出CD′的长,故可得出结论.
| CD |
| AD |
| 1 |
| 2 |
解答: 解:∵△ABC是等腰直角三角形,
解:∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵CA=CB=3,D是BC上一点,且
=
,
∴AD=2,CD=1,
作点D关于直线AB的对称点D′,连接CD′,
∵点D于点D′关于直线AB对称,
∴AD=AD′=2,∠DAD′=2∠BAC=90°,
在Rt△ACD′中,
CD′=
=
=
,
∴△CMD的周长的最小值=CD′+CD=
+1.
故选D.
 解:∵△ABC是等腰直角三角形,
解:∵△ABC是等腰直角三角形,∴∠BAC=45°,
∵CA=CB=3,D是BC上一点,且
| CD |
| AD |
| 1 |
| 2 |
∴AD=2,CD=1,
作点D关于直线AB的对称点D′,连接CD′,
∵点D于点D′关于直线AB对称,
∴AD=AD′=2,∠DAD′=2∠BAC=90°,
在Rt△ACD′中,
CD′=
| AD′2+AC2 |
| 22+32 |
| 13 |
∴△CMD的周长的最小值=CD′+CD=
| 13 |
故选D.
点评:本题考查的是轴对称-最短路线问题,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
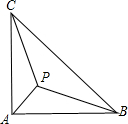 如图,在等腰直角三角形ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC=
如图,在等腰直角三角形ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC= 23、如图,在等腰直角三角形ABC和DEC中,∠BCA=∠BCE=90°,点E在边AB上,ED与AC交于点F,连接AD.
23、如图,在等腰直角三角形ABC和DEC中,∠BCA=∠BCE=90°,点E在边AB上,ED与AC交于点F,连接AD.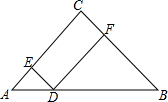 (2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( )
(2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( ) 如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.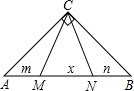 如图,在等腰直角△ABC的斜边AB上取两点M、N(不与A、B重合)使∠MCN=45°,记AM=m,MN=x,NB=n,试判断以x、m、n为边长的三角形的形状,并给予说明.
如图,在等腰直角△ABC的斜边AB上取两点M、N(不与A、B重合)使∠MCN=45°,记AM=m,MN=x,NB=n,试判断以x、m、n为边长的三角形的形状,并给予说明.