��Ŀ����
��֪��������y=ax2+bx+c(a��0)��ͼ����B(12,0)��C(0��-6�����Գ���Ϊx=2.

(1)��������ߵĽ���ʽ��
(2)��D���߶�AB����AD=AC��������P��A�������߶�AB��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ��һ����Q��ijһ�ٶȴ�C�������߶�CB�����˶������Ƿ����ijһʱ�̣�ʹ�߶�PQ��ֱ��CD��ֱƽ�֣������ڣ��������ʱ��ʱ��t���룩�͵�Q���˶��ٶȣ��������ڣ���˵�����ɣ�
(3)�ڣ�2���Ľ����£�ֱ��x=1���Ƿ���ڵ�M��ʹ��MPQΪ���������Σ������ڣ���������е�M�����ꣻ����������˵������.
��������
�����������1���ѵ�B��C��������������߽���ʽ�����ݶԳ������ʽ�г�����a��b��c�ķ����飬��⼴�ɣ���2�����������߽���ʽ�����A�����꣬�����ù��ɶ�����ʽ���AC�ij���Ȼ�����OD���ɵõ�D�������߶Գ����ϣ������߶δ�ֱƽ�����ϵ����ʿɵá�PDC=��QDC��PD=DQ���ٸ��ݵȱ߶ԵȽǿɵá�PDC=��ACD���Ӷ��õ���QDC=��ACD���ٸ����ڴ�����ȣ���ֱ��ƽ�пɵ�PQ��AC���ٸ��ݵ�D�ڶԳ������жϳ�DQ�ǡ�ABC����λ�ߣ����������ε���λ��ƽ���ڵ����߲��ҵ��ڵ����ߵ�һ�����DQ= AC�������AP��Ȼ�����ʱ��=·�̡��ٶ������P�˶���ʱ��t�����ݹ��ɶ������BC��Ȼ�����CQ�������ٶ�=·�̡�ʱ�䣬���㼴�������Q���ٶȣ���3��������������ĵ�M��ʹ�á�MPQΪ���������Σ���ô����ҪҪ�������ۣ��ٵ�MP=MQ����MΪ���㣻�ڣ���PQΪ������MPQ����ʱ����PΪ���㣻�۵�PQΪ������MPQ����ʱ����QΪ����.���з�����⼴��.
AC�������AP��Ȼ�����ʱ��=·�̡��ٶ������P�˶���ʱ��t�����ݹ��ɶ������BC��Ȼ�����CQ�������ٶ�=·�̡�ʱ�䣬���㼴�������Q���ٶȣ���3��������������ĵ�M��ʹ�á�MPQΪ���������Σ���ô����ҪҪ�������ۣ��ٵ�MP=MQ����MΪ���㣻�ڣ���PQΪ������MPQ����ʱ����PΪ���㣻�۵�PQΪ������MPQ����ʱ����QΪ����.���з�����⼴��.
����������⣺����һ���������߹�C(0,-6)
��c=��6, ��y=ax2+bx��6
�� ����ã�a=
����ã�a= ,b=��
,b=��
��������ߵĽ���ʽΪy= x2��
x2�� x��6��
x��6��
����������A��B����x=2�Գ�
��A����8��0������y=a(x��8)(x��12)
C���������ϣ��࣭6=a��8��(��12) ��a=
��������ߵĽ���ʽΪ��y= x2��
x2�� x��6.
x��6.
��2�����ڣ���ֱ��CD��ֱƽ��PQ,
��Rt��AOC��AC= =10=AD
=10=AD
���D�ڶԳ����ϣ�����DQ ��Ȼ��PDC=��QDC��
����֪��PDC=��ACD��
���QDC=��ACD����DQ��AC��
DB=AB��AD=20-10=10
��DQΪ��ABC����λ�ߣ���DQ= AC=5.
AC=5.
AP=AD-PD=AD-DQ=10-5=5
��t=5��1=5(��)
�����t=5(��)ʱ���߶�PQ��ֱ��CD��ֱƽ��,
��Rt��BOC��, BC= =6
=6 ��CQ=3
��CQ=3
���Q���˶��ٶ�Ϊÿ�� ��λ����.
�����.
��3������ ����Q��QH��x����H����QH=3��PH=9
��Rt��PQH��PQ= =3
=3 .
.
�ٵ�MP=MQ����MΪ���㣬
��ֱ��CD��ֱ�߷���Ϊ��y=kx+b(k��0),��
 ,��ã�
,��ã� .
.
��y=3x-6
��x=1ʱ��y=��3 , ��M1(1, ��3).
�ڵ�PQΪ������MPQ����ʱ����PΪ����.
��ֱ��x=1�ϴ��ڵ�M(1,y) ,�ɹ��ɶ����ã�
42+y2=90 ��y=��
��M2��1�� �� M3��1����
�� M3��1���� ��.
��.
�۵�PQΪ������MPQ����ʱ����QΪ����.
����Q��QE��y����E����ֱ��x=1��F����F(1, ��3)
��ֱ��x=1���ڵ�M(1,y), �ɹ��ɶ����ã�
(y��3)2+52=90
��y=��3��
��M4(1,
��3�� ) M5((1, ��3��
) M5((1, ��3�� ) .
) .
����������������������㣺
M1(1, ��3), M2��1�� ��, M3��1����
��, M3��1���� ��, M4(1, ��3��
��, M4(1, ��3�� ),
),
M5((1, ��3�� )
)

���㣺���κ����ۺ���.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�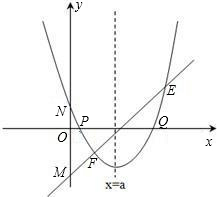 ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�
���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ� ��2013•��������֪��ֱ��y=ax+b��������y=-x2-2x+3�Ķ���P����ͼ��ʾ��
��2013•��������֪��ֱ��y=ax+b��������y=-x2-2x+3�Ķ���P����ͼ��ʾ��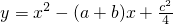 ������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ�
������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ� ����������x�ύ�ڵ�P��Q�����Ƿ�
����������x�ύ�ڵ�P��Q�����Ƿ� ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�
���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ� ������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ�
������a��b��c�ǡ�ABC�ġ�A����B����C�ĶԱߣ�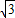 ����������x�ύ�ڵ�P��Q�����Ƿ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�
����������x�ύ�ڵ�P��Q�����Ƿ���ڹ�P��Q��������y�����е�Բ�������ڣ����Բ��Բ�����꣬�������ڣ���˵�����ɣ�