题目内容
如图,已知PA、PB是⊙O的两条切线,A、B是切点,连接OP.(1)求证:PA=PB;
(2)若⊙O的半径为2,PA=2
 ,求阴影部分面积.
,求阴影部分面积.
【答案】分析:(1)连接OA、OB,利用切线的性质和全等三角形的证明方法证明Rt△PAO≌Rt△PBO即可;
(2)利用三角形的面积公式及扇形的面积公式求出四边形PAOB的面积与扇形OAB的面积,两者相减即可求出阴影部分的面积.
解答:(1)证明:连接OA、OB,
∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAP=∠OBP=90°.
又∵OA=OB,
在Rt△PAO和Rt△PBO中,
∵PO=PO,OA=OB,
∴Rt△PAO≌Rt△PBO(HL).
∴PA=PB;
(2)解:由(1)知△PAO≌△PBO,
∴∠APO=∠BPO,∠AOP=∠BOP.
在Rt△PAO中,OA=2,PA=2 ,
,
tan∠APO= =
= ,
,
∴∠APO=30°,∠AOP=60°.
∴∠AOB=120°,
S阴影=S四边形APBO-S扇形=2S△PAO-S扇形=2× ×2×2
×2×2 -
- =4
=4 -
- .
.
点评:此题考查了切线的性质,直角三角形的性质及阴影部分面积的求法.阴影部分面积的求法是:规则图形根据面积公式来求;不规则图形采用“割补凑正法”,即将不规则的图形通过割补拼凑成一个或几个规则的图形,从而求出阴影部分面积.遇到切线,往往连接圆心与切点,构造直角三角形来解题.
(2)利用三角形的面积公式及扇形的面积公式求出四边形PAOB的面积与扇形OAB的面积,两者相减即可求出阴影部分的面积.
解答:(1)证明:连接OA、OB,

∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAP=∠OBP=90°.
又∵OA=OB,
在Rt△PAO和Rt△PBO中,
∵PO=PO,OA=OB,
∴Rt△PAO≌Rt△PBO(HL).
∴PA=PB;
(2)解:由(1)知△PAO≌△PBO,
∴∠APO=∠BPO,∠AOP=∠BOP.
在Rt△PAO中,OA=2,PA=2
 ,
,tan∠APO=
 =
= ,
,∴∠APO=30°,∠AOP=60°.
∴∠AOB=120°,
S阴影=S四边形APBO-S扇形=2S△PAO-S扇形=2×
 ×2×2
×2×2 -
- =4
=4 -
- .
.点评:此题考查了切线的性质,直角三角形的性质及阴影部分面积的求法.阴影部分面积的求法是:规则图形根据面积公式来求;不规则图形采用“割补凑正法”,即将不规则的图形通过割补拼凑成一个或几个规则的图形,从而求出阴影部分面积.遇到切线,往往连接圆心与切点,构造直角三角形来解题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
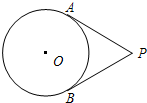 如图,已知PA、PB都是⊙O的切线,A、B为切点,且∠APB=60°.若点C是⊙O异于A、B的任意一点,则∠ACB=( )
如图,已知PA、PB都是⊙O的切线,A、B为切点,且∠APB=60°.若点C是⊙O异于A、B的任意一点,则∠ACB=( )| A、60° | B、120° | C、60°或120° | D、不能确定 |
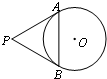 9、如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是
9、如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是 5、如图,已知PA、PB切⊙O于点A、B,OP交AB于C,则图中能用字母表示的直角共有( )个.
5、如图,已知PA、PB切⊙O于点A、B,OP交AB于C,则图中能用字母表示的直角共有( )个. 如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC的大小是( )
如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC的大小是( ) (2012•锦州二模)如图,已知PA、PB是⊙O的两条切线,A、B是切点,连接OP.
(2012•锦州二模)如图,已知PA、PB是⊙O的两条切线,A、B是切点,连接OP.