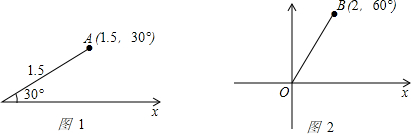Question

如图1，在平面内有射线Ox和一点A，连接OA，若OA=1.5，∠AOx=30°，则可用（1.5，30°）表示点A的位置，如图2，在平面内有一点B（2，60°），以O为坐标原点，以Ox为x轴建立平面直角坐标系，求点B在平面直角坐标系xOy内的坐标。

Answer 1

解：作BC⊥OX于点C，
∵OB=2，∠BOX=60°，
∴OC=OB×cos60°=1，BC=OB×sin60°=，
∴点B在平面直角坐标系xOy内的坐标为：（1，）。