题目内容
 如图,在直角坐标系中,直线
如图,在直角坐标系中,直线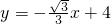 分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠ABO=30°,AB=4,将△ABO绕原点O顺时针旋转180°,在旋转过程中,当AB与直线MN平行时点A的坐标为
分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠ABO=30°,AB=4,将△ABO绕原点O顺时针旋转180°,在旋转过程中,当AB与直线MN平行时点A的坐标为
- A.(1,
 )
) - B.(
 ,1)
,1) - C.(
 ,-1)
,-1) - D.(1,
 )
)
B
分析:首先根据题意作出旋转后的图形,设BA的延长线交x轴于点D,过点A作AC⊥OA于点C,由∠ABO=30°,AB=4,可求得∠BAO的度数,OA的长,又由直线MN的解析式为y=- x+4,AB∥MN,可求得∠AOD=∠ADO=30°,继而可求得点A的坐标.
x+4,AB∥MN,可求得∠AOD=∠ADO=30°,继而可求得点A的坐标.
解答: 解:如图,设BA的延长线交x轴于点D,过点A作AC⊥OA于点C,
解:如图,设BA的延长线交x轴于点D,过点A作AC⊥OA于点C,
∵AB=4,∠ABO=30°,
∴OA= AB=2,∠BAO=90°-∠ABO=60°,
AB=2,∠BAO=90°-∠ABO=60°,
∴∠OAD=120°,
∵直线MN的解析式为y=- x+4,
x+4,
∴tan∠NMO= ,
,
∴∠NMO=30°,
∵AB∥MN,
∴∠ADO=∠NMD=30°,
∴∠AOC=30°,
∴AC= OA=1,
OA=1,
∴OC= =
= ,
,
∴点A的坐标为( ,1).
,1).
故选B.
点评:此题考查了一次函数的应用、含30°的直角三角形的性质以及等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
分析:首先根据题意作出旋转后的图形,设BA的延长线交x轴于点D,过点A作AC⊥OA于点C,由∠ABO=30°,AB=4,可求得∠BAO的度数,OA的长,又由直线MN的解析式为y=-
 x+4,AB∥MN,可求得∠AOD=∠ADO=30°,继而可求得点A的坐标.
x+4,AB∥MN,可求得∠AOD=∠ADO=30°,继而可求得点A的坐标.解答:
 解:如图,设BA的延长线交x轴于点D,过点A作AC⊥OA于点C,
解:如图,设BA的延长线交x轴于点D,过点A作AC⊥OA于点C,∵AB=4,∠ABO=30°,
∴OA=
 AB=2,∠BAO=90°-∠ABO=60°,
AB=2,∠BAO=90°-∠ABO=60°,∴∠OAD=120°,
∵直线MN的解析式为y=-
 x+4,
x+4,∴tan∠NMO=
 ,
,∴∠NMO=30°,
∵AB∥MN,
∴∠ADO=∠NMD=30°,
∴∠AOC=30°,
∴AC=
 OA=1,
OA=1,∴OC=
 =
= ,
,∴点A的坐标为(
 ,1).
,1).故选B.
点评:此题考查了一次函数的应用、含30°的直角三角形的性质以及等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: