题目内容
如图,巳知△ABC是面积为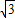 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).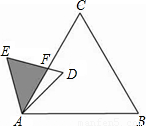
【答案】分析:根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,再根据求出其边长,可根据三角函数得出三角形面积.
解答: 解:∵△ABC∽△ADE,AB=2AD,
解:∵△ABC∽△ADE,AB=2AD,
∴ =
= ,
,
∵AB=2AD,S△ABC= ,
,
∴S△ADE= ,
,
在△EAF中,作HF⊥AE交AE于H,
则∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°= x.
x.
又∵S△ADE= ,
,
作CM⊥AB交AB于M,
∵△ABC是面积为 的等边三角形,
的等边三角形,
∴ ×AB×CM=
×AB×CM= ,
,
∠BCM=30°,
AB=2k,BM=k,CM= k,
k,
∴k=1,AB=2,
∴AE= AB=1,
AB=1,
∴x+ x=1,
x=1,
解得x= =
= .
.
∴S△AEF= ×1×
×1× =
= .
.
点评:此题主要考查相似三角形的判定与性质和等边三角形的性质等知识点,解得此题的关键是根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,然后问题可解.
解答:
 解:∵△ABC∽△ADE,AB=2AD,
解:∵△ABC∽△ADE,AB=2AD,∴
 =
= ,
,∵AB=2AD,S△ABC=
 ,
,∴S△ADE=
 ,
,在△EAF中,作HF⊥AE交AE于H,
则∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°=
 x.
x.又∵S△ADE=
 ,
,作CM⊥AB交AB于M,
∵△ABC是面积为
 的等边三角形,
的等边三角形,∴
 ×AB×CM=
×AB×CM= ,
,∠BCM=30°,
AB=2k,BM=k,CM=
 k,
k,∴k=1,AB=2,
∴AE=
 AB=1,
AB=1,∴x+
 x=1,
x=1,解得x=
 =
= .
.∴S△AEF=
 ×1×
×1× =
= .
.点评:此题主要考查相似三角形的判定与性质和等边三角形的性质等知识点,解得此题的关键是根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,然后问题可解.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
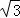 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 _________ (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 _________ (结果保留根号).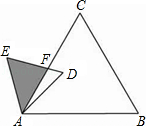
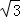 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 _________ (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 _________ (结果保留根号).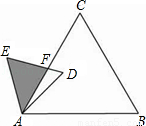
 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).