题目内容
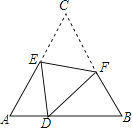
【题目】如图,在边长为6的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则OF的长为 . 
【答案】![]()
【解析】解:过点E作EG⊥BD于点G,
∵四边形ABCD是正方形,
∴∠GBE=45°,
∴△BEG是等腰直角三角形.
∵BE= ![]() BC=3,
BC=3,
∴ ![]() ,
,
∵BD= ![]() ,
,
∴DO= ![]() ,DE=
,DE= ![]() -
- ![]() =
= ![]() ,
,
∵∠DOF=∠DGE =90°,∠ODF=∠GDE,
∴△DOF∽△DGE,
∴ ![]() ,
,
即 ![]() ,
,
∴ ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目