题目内容
正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.

1.求证:△DEF∽△CEB;
2.当点P运动到DA的中点时,求证:点F为DC的中点.
1.∵ DE⊥CP,EF⊥BE,
∴ ∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,
∴ ∠1=∠2. ……………………………(2分)
∵ 四边形ABCD是正方形,∴ ∠4+∠6=∠DCB=90°,
在Rt△DEC中,∠4+∠5=90°,
∴ ∠5=∠6, ……………………………(5分)
∴ △DEF∽△CEB. ……………………………(6分)

2.∵ 四边形ABCD是正方形,
∴ 当点P运动到DA的中点时,PD=![]() AD=
AD= DC.
DC.
∴ 在Rt△PDC中,tan∠4=![]() ,
,
∵ 在Rt△DEC中,tan∠4=![]() ,
,
∴ ![]() . ……………………………(9分)
. ……………………………(9分)
∵ △DEF∽△CEB,
∴ ![]() . ……………………………(11分)
. ……………………………(11分)
∵ CB=DC,
∴ ![]()
∴ 点F为DC的中点. ……………………………(12分)
(注:用其它方法求解参照以上标准给分.)
解析:略

练习册系列答案
相关题目
 17、已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为
17、已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为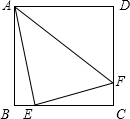 如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于
如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于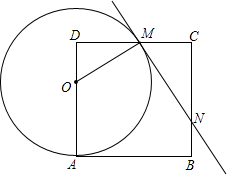 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.